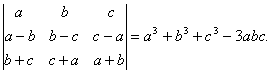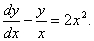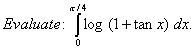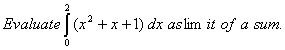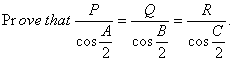CBSE Guess > Papers > Question Papers > Class XII > 2006 > Mathematics > Delhi Set - I.
Mathematics — 2006 (Set I — Delhi)
SECTION - A
Q. 1. Express the following matrix as the sum of a symmetric and a skew symmetric matrix.
Q. 2. Using properties of determinants, prove the following:
Q. 3. Solve the following differential equation:
Q. 4. Form the differential equation of the family of curves y = a sin (x + b), where a and b are arbitrary constants.
Or
Solve the following differential equation:
2xy dx + (x2 + 2y2) dy = 0.
Q. 5.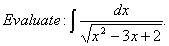 
Q. 6. 
Q. 7. Two dice are rolled once. Find the probability that:
- the numbers on two dice are different
- the total of numbers on the two dice is at least 4
Q. 8. A pair of dice is tossed twice. If the random variable X is defined as the number of doublets, find the probability distribution of X.
Q. 9. Examine the validity of the following argument:
Or
Q. 10. Differentiate sin (2x + 3) w. r. t. x from first principle.
Q. 11. 
Q. 12.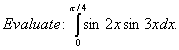 
Or
Q. 13.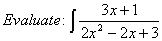 
Q. 14.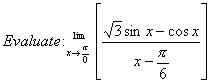 
Q. 15. Verify Rolle’s Theorem for the following function: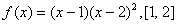 
Q. 16. Using matrices, solve the following systern of equations:
x + y + z = 3; x - 2y + 3z = 2 and 2x - y + z = 2.
Q. 17. Find the point on the curve y2 = 4x which is nearest to the point (2, -8).
Or
Prove that the height of a right circular cylinder of maximum volume that can be inscribed in a sphere of radius R is
, Also find the maximum volume.
Q. 18. Find the area of the region bounded by y = 4x, x = 1, x = 4 and x-axis in the first quadrant.
Or
SECTION - B
Q. 19.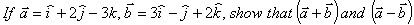 
are perpendicular to each other:
Q. 20. Using vectors, prove that the line segment joining the mid-point of non-parallel sides of a trapezium is parallel to the base and is equal to half the sum of the parallel sides.
Q. 21. A body moving with a velocity of 36 km/hour, is brought to rest in 10 seconds. Find the retardationand the distance traveled by the body before to rest.
Q. 22. A particle is projected so as to graze the tops of two walls, each of height 10 m at 15m and 45 mrespectively from the point of projection. Find the angle of projection.
Or
P, Q, R, S are points in a vertical line so that P is the highest and PQ = RS. If a body falls from rest at P, prove that the times of describing the successive intervals are in the ratio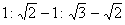 
Q. 23. ABC is a given triangle in which forces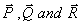 
act along OA, OB and OC, where O is the incentre of the triangle, are in equilibrium.
Q. 24. Two like parallel forces 
act on a rigid body at A and B respectively. If are interchanged in position, show that the point of application of the resultant will be displaced through a distance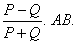 
Q. 25. Find the equation of the plane passing through the points (1, 2, 3) and (0, -1, 0) and parallel to the line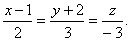 
Or
Find the vector and Cartesian equation of the sphere described on the join of the points (2, -3, 4) and (-5, 6, -7)as the extremities of a diameter.
Q. 26. The vector equations of two lines are:
SECTION – C
Q. 19. In a factory, which manufactures nuts, machines A, B and C manufacture respectively 25%, 35% and 40% of nuts. Of their output 5, 4 and 2 per cent respectively are defective nuts. A nut is drawn at random from the product and is found to be defective. Find the probability that it is manufactured by machine B.
Q. 20. If the mean and variance of the binomial distribution are respectively 9 and 6, find the distribution.
Or
8% of people in a group are left handed. What is the probability that 2 or more of a random sample of 25 from the group are left handed?
Q. 21. What is the face value of a bill discounted at 5% per annum 73 days earlier than its legal due date, the banker’s gain being Rs.10?
Q. 22. A bill for Rs. 21,900 drawn on July 10, 2005 for 6 months, was discounted for Rs. 21,720 at 5% per annum. On what date was the bill discounted?
Q. 23. A and B are partners sharing profits and losses in the ratio 3 : 4 respectively. They admit C as a new partner, the new profit sharing ratio being 2 : 2 : 3 between A, B and C respectively. C pays Rs. 12,000 as premium for goodwill. Find the amount of premium shard by A and B.
Q. 24. Find the present worth of an ordinary annuity of Rs. 1,200 per annum for 10 years at 12% per annum, compounded annually.
[Use (1.12)-10 = 0.3221].
Q. 25. If the total cost function is given by C = a + bx + cx2 where x is the quantity of output, show that
If the marginal revenue function for a commodity is MR = 9 – 6x2 + 2x, find the total revenue function and the corresponding demand function.
Q. 26. A dealer wishes to purchase a number of fans and sewing machines. He has only Rs. 5,760 to invest and has space for at most 20 items. A fan and sewing machine cost Rs. 360 and Rs. 240 respectively. He can sell a fan at a profit of Rs. 22 and sewing machine at a profit of Rs. 18. Assuming that he can sell whatever he buys, how should he invest his money in order to maximise his profit? Trans late the problem into LPP and solve it graphically.
| Mathematics 2006 Question Papers Class XII | |||||||
| Delhi | Outside Delhi | Compartment Delhi | Compartment Outside Delhi | ||||
 |
Set I | |
Set I | |
Set I | |
Set I |
|
Set II | |
Set II | |
Set II | |
Set II |
|
Set III | |
Set III | ||||
