CBSE Guess > Papers > Question Papers > Class XII > 2003 > Mathematics > Compartment Outside Delhi Set -I

MATHEMATICS—2003 (Set I—Compartment Outside Delhi)

Q. 1. Show that the differential equation of all parabolas is given by

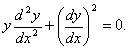
Q. 2. Find the values of 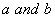for which the following holds:

Q. 3. Evaluate: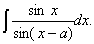

Q. 5. Evaluate: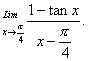

Q. 6. Using properties of determinants, show that

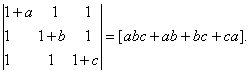
Q. 7. If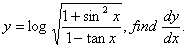

Or

If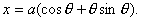

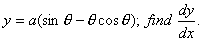
Q. 8. Solve the following differential equation: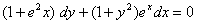

Or

Solve the following differential equation: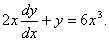

Q. 9. Evaluate: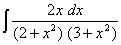

Q. 10. Evaluate: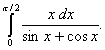

Or

Evaluate: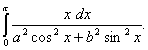

Q. 11. Find the intervals in which the function is (a) increasing, (b) decreasing.

Q. 12. If P (A) = 0.3, P (B) = 0.7 and P (B/A) = 0.5, find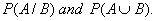

Q. 13. For the curve 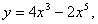find all points at which the tangent passes through the origin.

Q. 14. The two lines of regression are given by 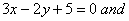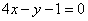Find 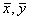. and the co-efficient of correlation between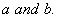

Q. 15. A box contains100 bolts and 50 nuts. It is given that 50% bolts and 50% nuts are rusted. Two objects are selected from the box random. Find the probability that both are both or are rusted.

Or

The probability of A hitting a target is 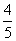and that of B hitting it is 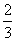they both fire at the target. Find the probability that
(i) At least one of them will hit the target
(ii) Only one of them will hit the target.

Q. 16. Find the area of the following region:

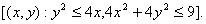
Q. 17. A window is in form of a rectangle surmounted by a semi-circle. If the perimeter of the window is 100m, find the dimensions of the window so that maximum light enters through the window.

Q. 18. Given that

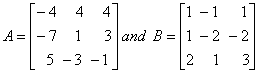
Find AB. Use this to solve the following system of linear equations:

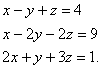
SECTION - B

  Q. 19. Find the values of so that the vectors 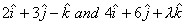are (i) parallel, (ii) perpendicular to each other.

Q. 20. Find the equations of the perpendicular from the point (3, -1, 11) to the line 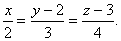Also find the foot of the perpendicular and the length of the perpendicular.

Q. 21. The resultant of two forces P and Q is equal to P in magnitude, and that of two forces 2P and Q (acting in the same direction as before) is also equal to P. Find the magnitude of Q.

Q. 22. A weight of 26 N is suspended by two light strings of lengths 5 m and 12 m from two points at the same level and 14 m apart. Find the tension in the strings.

Q. 23. Using vectors prove that angle in a semicircle is a right angle.

Q. 24. Solve the following differential equation: n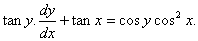

Q. 25. Find the shortest distance between two lines whose vector equations are given below:

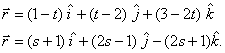
Q. 26. A particle was moving with a uniform acceleration. In the eleventh and fifteenth seconds from the start, it traveled 33 m and 39 m respectively. Find
(i) The initial velocity
(ii) The acceleration
(iii) The distance covered by the particle in 20 seconds
(iv) The distance covered by the particle in the 20 th second.

Or

A particle is projected so as to pass through two points whose horizontal distances from the points of projection are 12 m and 24 m and which are at vertical height of 4 m and 5 m respectively above the horizontal plane through the point of projection. Find the velocity and direction of projection.
(Use g = 10 m/sec ² )

SECTION - C

Q. 19. The first three moments about the value 5 of a variable are -4, 22, -117 respectively. Find the mean, variance and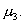

Q. 20. For a near normal distribution, find Bowley's co-efficient of skewness from the following information:

Q. 21. A, B and C enter into a partnership business. A invests one-fourth of the total capital for half of the total time, B invests one-third of the total capital for one-fourth of the total time and C invests the remaining capital for full time. Find the share of each in a profit of Rs. 30,000.

Q. 22. How much should a company set aside at the end of each year if it has to buy a machine expected to cost Rs. 2,00,000 at the end of 6 years. When the rate of interest is 10% per annum compounded annually? [Use (1.1) ⁶ = 1.772]

Q. 23. An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers and their probability of accidents are 0.01, 0.03 and 0.15 respectively. One of the insured persons meets with an accident. Find the probability that he is a scooter driver.

Q. 24. From a well shuffled pack of 52 cards. 3 cards are draw one-by-one with replacement. Find the probability distribution of number of queens.

Q. 25. The cost function of a firm is given by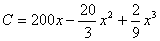
Where x is the output. Find the output at which the
(i) Average cost is minimum
(ii) Marginal cost is minimum
(iii) Marginal cost is the equal to average cost.

Q. 26. A company manufactures, two types of toys-A and B. Toy A requires 4 minutes for cutting and 8 minutes for assembling and Toy B requires 8 minutes for assembling. There are 3 hours and 20 minutes available in a day for cutting and 4 hours for assemble. The profit on a piece of toy A is Rs. 50 and that on toy B is Rs. 60. How many toys of each type should be made daily to have maximum profit? Solve the problem graphically.

Or

A shopkeeper deals in two items-thermos-flasks and air tight containers. A flask costs him Rs. 120 and an air tight container costs him Rs. 60. He has at the most Rs. 12,000 to invest and has space to store a maximum of 150 items. The profit on selling a flask is Rs. 20 and an air tight container is Rs. 15. Assuming that he will be able to sell all things h buys, how many of each items should he buy to maximise his profit? Solve the problem graphically.

Mathematics 2003 Question Papers Class XII
Delhi		Outside Delhi		Compartment Delhi		Compartment Outside Delhi
	Set I		Set I		Set I		Set I
	Set II		Set II		Set II		Set II
	Set III		Set III