CBSE Guess > Papers > Question Papers > Class XII > 2003 > Mathematics > Delhi Set -I

MATHEMATICS—2003 (Set I—Delhi)

Q. 1. Evaluate: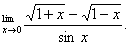

Q. 2. Differentiate the following w.r.t. x: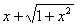

Q. 3. Evaluate"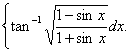

Q. 4. Evaluate: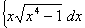

Or

Evaluate: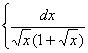

Q. 5. If 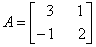, show that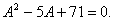

Q. 6. Form the differential equation of the following family of curves: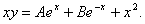

Q. 7. Solve the following differential equation: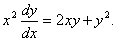

Or

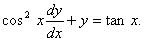
Q. 8. Using the properties of determinants, evaluate the following:

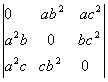
Q. 9. A balloon which always remains spherical is being inflated by pumping in gas at the rate of 900 cm ³ /sec. Find the rate at which the radius of the balloon is increasing when the radius of the balloon is 15cm

Q. 10. Evaluate: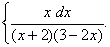

Q. 11. Evaluate: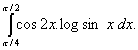

Q. 12. Find the derivative of 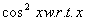from first principle.

Or

Find the derivative of 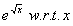from first principle.

Q. 13. A bag contains 5 red, 6 white and 7 black balls. Two balls are drawn at random. What is the probability that both balls are red or both are black?

Or

A die is thrown twice and the sum of the numbers appearing is observed to be 8. What is the conditional probability that the number 5 has appeared at least once?

Q. 14. Show that there is no correlation between the variables x and y in the following data:

Q. 15. In a correlation analysis, the following values are obtained about the variables x and y.

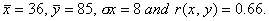
Find the equations of the regression lines and estimate the value of y when x = 30.

Q. 16. A square piece of tin of side 18 cm is to be made into box without a top by cutting a square piece from each corner and folding up the flaps. What should be the side of the square to be cut off, so that the volume of the box be maximum? Also find the maximum volume of the box.

Q. 17. Find the area of the region lying between the parabolas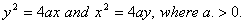

Q. 18. Using matrix method, solve the following equations:

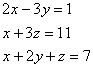
SECTION - B

Q. 19. The dot product of a vector with the vectors 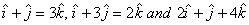are 0, 5 and 8 respectively. Find the vector.

Q. 20. Using vectors, prove that the mid-point of the hypotenuse of a right-angled triangle is equidistant from its vertices.

Q. 21. Three forces 5 P, 10 P and 13 P in a plane act on a particle. The angle between any two of them is 120⁰. Find the magnitude and direction of the resultant,

Q. 22. A body has a velocity of 15 m/sec at a certain instant and 10 seconds later, it has a velocity of 45 m/sec. If the velocity changes uniformly, Find the distance by the body.

Q. 23. Solve the following differential equation: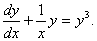

Q. 24. Find the vector equation of the line passing through the point A (2, -1, 1) and parallel to the line joining the points B (-1, 4, 1) and C (1, 2, 2). Also find the Cartesian equation of the line.

Q. 25. Find the equation of the plane passing through the point (1, 1, 1) and perpendicular to each of the following planes: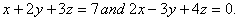

Q. 26. A short fired at a mark in the horizontal plane through the point of projection, goes 'a' m beyond if when the angle of elevation is 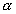. When the angle of elevation is 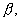it falls 'b' m short of the mark. Show that the proper elevation to hit the mark is

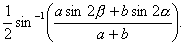
Or

A particle is projected so as to have a range R on a horizontal plane through the point of projection. If 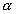and 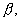are the possible angles of projection and 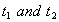are corresponding times of flight, Show that

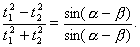
SECTION - C

Q. 19. Find the first three moments about the value 5 for the following set of numbers: 3, 5, 7, 9, 11

Q. 20. A company has two plants to manufacture bicycles. The first plant manufactures 60% of the bicycles and the second plant 40%. 80% of the bicycles are rated of standard quality at the first plant and 90% of standard quality at the second plant. A bicycle is picked up at random and found to be of standard quality. Find the probability that it comes from the second plant.

Q. 21. Find the amount of an annuity of Rs. 2,000 payable at the end of each 3 months for 6 years, If money is worth 8% per annum compounded quarterly. [Use (1.02)²⁴ =1.608]

Q. 22. A merchant in London buys dollars when 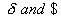rate is 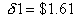and sells when it falls to 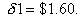. If he makes a profit of 450 in the transaction, find his original investment.

Q. 23. Calculate the Kari Pearson's coefficient of skewness from the following data:

Q. 24. Six coins are tossed simultaneously. Find the probability of getting
(i) 3 heads
(ii) no heads
(iii) at least one head.

Q. 26. A company manufactures two articles A and B. There are two departments through which these articles are processed: (i) assembly and (ii) finishing departments. The maximum capacity of the first department is 48 hours a week. The production of each article A requires 4 hours in assembly and 2 hours in finishing and that of each unit of B requires 2 hours in assembly and 4 hours in finishing. If the profit is Rs. 6 for each unit of A and Rs. 8 for each unit of B, Find the number of units of A and B to be produced per week in order to have maximum profit.

Or

A factory owner wants to purchase two types of machines, A and B, for his factory, The machine A requires an area of 1000 m ² and 12 skilled men for running it and its daily output is 40 units. If an area of 7600 m ² and 72 skilled men be available to operate the machine, how many machines of each should be bought to maximize the daily output?

Mathematics 2003 Question Papers Class XII
Delhi		Outside Delhi		Compartment Delhi		Compartment Outside Delhi
	Set I		Set I		Set I		Set I
	Set II		Set II		Set II		Set II
	Set III		Set III