Example 1
The magnitude of the induced emf 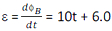
At t = 2.0 s, ε = 10 x 2 + 6.0 = 26 mV
Example 2
The magnitude of the induced emf
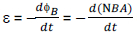
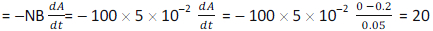 volt
volt
Example 3
The magnitude of the induced emf 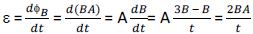
Example 4
The magnetic flux passing through the loop is given by ΦB = BA cosθ = B0 sin ωt x πr2 x cos 00 = B0 πr2 sin ωt
The magnitude of the induced emf, 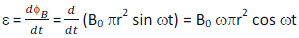
The magnitude of the induced current, 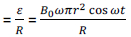
Example 5
The reading of the millivoltmeter = motional emf produced across the axle = Bvl
Speed v = 135 km/h = 135 x 5/18 m/s = 37.5 m/s
Magnetic field B = 0.2 G = 0.2 x 10- 4 T
Length l = 1 m
Therefore, the reading of the millivoltmeter = 0.2 x 10- 4 x 37.5 x 1 = 0.00075 V = 0.75 mV
Example 6
Wing span l = 50 m
Speed v = 200 m/s
Horizontal component of earth's field BH = 0.3 gauss = 0.3 x 10- 4 T
Vertical component of earth's field BV = 0.5 gauss = 0.5 x 10- 4 T
An aeroplane flying horizontally cuts only the vertical component of the earth's field. So, the potential difference
between the wing tips of the aeroplane is
ε = Bvvl = 0.5 x 10- 4 x 200 x 50 = 0.5 V
Example 7
The network of resistors forms a balanced Wheatstone bridge and hence resistor of 3 ohm in the middle can
be neglected. Remaining resistors have an equivalent resistance = 3 ohm. Total resistance = 3 + 1 = 4 ohm.
Induced emf, Bvl = IR
Or 2 x v x 0.10 = 1 x 10- 3 x 4
This gives v = 2 cm/sec.
Example 8
The initial magnetic flux enclosed by the rod and the rails (at time t = 0) = BA = B0x0l.
The induced emf is given by 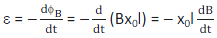
As a result of the induced emf a current will flow through the rod with a magnitude equal to 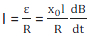
The direction of the current is along the wire, and therefore perpendicular to the magnetic field. The force
exerted by the magnetic field on the rod is given by 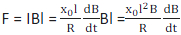
The acceleration of the rod is therefore given by 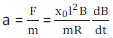
Example 9
Emf induced between the rim and the axle is
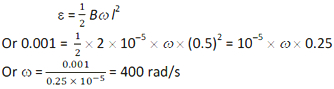
Example 10
Length of rod l = 1 m
Speed v = 72 km/h = 20 m/s
Angle of dip δ = 300
A rod falling vertically along east-west direction cuts only the horizontal component of the earth's field.
Vertical component of earth's field Bv = 1/2 √3 gauss = (1/2 √3) x 10- 4 T
Horizontal component of earth's field BH = Bv / tan δ = (1/2 √3)/(1 / √3) gauss = 0.5 x 10-4 T
So, the potential difference between the ends of is
ε = BHvl = 0.5 x 10- 4 x 20 x 1 = 10- 3 V
CBSE Electromagnetic Induction ( With Hint / Solution)
Class XII (By Mr. Ashis Kumar Satapathy)
email - [email protected]
Electromagnetic Induction