As we know, work has to be done against the back emf in establishing the current through an inductor. This work done is stored as magnetic potential energy in the coil (inductor). The rate of work when a current I flows through the inductor is given by
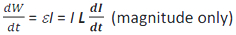
Therefore,
dW = LIdI
Total amount of work done in establishing the current I is W = ∫ dw = ∫0I LIDI
By integrating it, we get w=1/2 LI2
Therefore, magnetic potential energy in s inductor
(solenoid) is given by 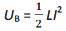
The self inductance if a solenoid is L= μ 0n2 Al
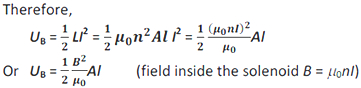
Al is the volume of the solenoid. Therefore, the energy density (energy per unit volume) is given 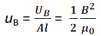
This relation has been derived for a solenoid but it is general and valid for any region of space in
which a magnetic field exists.
Recall that the electrostatic energy stored per unit volume in a parallel plate capacitor is given
by 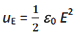
It should be noted that in both the cases energy is proportional to the square of the field strength. Both are general relations.
NOTE :
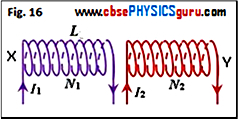
If electric currents are flowing simultaneously in two nearby coils, the flux linked with one coil will be the sum of two fluxes which exist independently in two coils. Therefore, total flux linkages with coil X is given by (See figure 16)

CBSE Electromagnetic Induction ( With Hint / Solution)
Class XII (By Mr. Ashis Kumar Satapathy)
email - [email protected]
Electromagnetic Induction