Motional Electromotive Force

If a rod of length l moves with velocity v in a direction perpendicular to a uniform and time independent magnetic field B, an emf is induced in the rod.

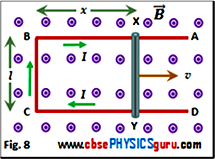
As shown in figure 8 rod XY is free to move on a conductor ABCD. The rod XY is moved towards the right with a constant velocity v. Assume that the rod XY and the conductor ABCD is frictionless so that there is no loss of energy. The area enclosed by XBCY changes as the rod XY moves. The uniform magnetic field B is perpendicular to the plane of the area XBCY. Let the length XB be x. As the area enclosed by XBCY changes, the magnetic flux enclosed by the loop changes. The magnetic flux enclosed by the loop XBCY is given by

Φ_B = BA cos θ = BA cos 0⁰ = BA = Blx

As the magnetic flux is changing, an emf will be induced. This induced emf is given by

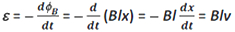
where dx/dt = –v is the speed of the rod XY.
The induced emf Blv is called motional emf as it is induced by moving a rod or conductor instead of varying the magnetic field.

The motional emf can also be explained on the basis of the Lorentz force acting on the free charge carriers (free electrons) of rod XY. When the rod moves with velocity v in a uniform magnetic field B, a force is exerted on the electrons (qvB in magnitude) along the length of the rod towards end X so that one end (here, end X) becomes negatively charged and the other end positively charged (end Y). This in turn sets up a nonconservative electrical field in the conductor. The strength of this electric field increases until the electrostatic force produced by this field is equal in magnitude to the magnetic force. At this point the upward flow of electrons stops and equilibrium is attained. In equilibrium of charges inside the rod,

electric force = magnetic force
e E = e vB
E = v B
This creates a potential difference between two ends given by
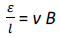
Thus, induced emf ε = v B l

Looking at figure 8 we observe that vl is the area swept across by the rod per second. The quantity Bvl is the magnetic flux swept across by the rod per second. Thus, emf
ε = Rate of sweeping of magnetic flux

If the resistance of rod XY be R and that of arms XB, BC and CY be negligible as compared to R, then the current I in the loop is given by

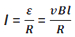
As the magnetic field is also present, the magnetic force F = IBl acts on the rod XY. This force is directed opposite to the velocity of the rod XY. Thus,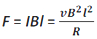

As we know this force originates due to drift velocity of charges which is responsible for current along the rod and the consequent Lorentz force acting on them.
The power required to move the rod XY with a constant speed v is given by

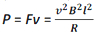
NOTE :-

1. The lower end Y of the rod XY is at higher potential compared to the upper end X but the current in the rod flows from upper end (low potential) to lower end (higher potential) because the rod acts as a source of emf and current inside a source of emf is from lower potential to higher potential.


2. If any two of the quantities, v, B or l are parallel, no induced emf is produced.


3. If a conductor moves vertically up or down with its length in east-west direction, it cuts the horizontal component of earth's magnetic field.


4. If a conductor moves vertically up or down with its length in north-south direction, it does not ut any component of earth's magnetic field.


5. If a conductor moves horizontally in any direction, it cuts vertical component earth's magnetic field.


6. If a conducting rod XY of length l is rotated about one end perpendicular to a uniform magnetic field B with constant angular velocity ω (figure 9), the induced emf between two ends of the rod can be calculated by considering a small element of the rod dr at a distance r from the end X. The linear velocity is different for different elements but angular velocity is same for all elements. The emf induced across the element dr is given by
   

   dε = Bvdr= Brω dr [ Using v = rω ]
   Therefore, the emf induced across the end of the rod XY is given by
   
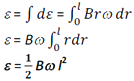
   If f be the frequency of rotation of the rod, then putting ω = 2Πf, we get
   

7. If, in the case above, a wheel having spokes, each of length l rotates in a magnetic field, the potential difference between the centre of the wheel and a point on the rim (circumference) will be given by the same equation.
   It should be noted that the number of spokes is immaterial because the emf's across the spokes are in parallel.


8. If a disc rotates in a magnetic field, the potential difference between the centre of the disc and a point on the circumference will be given by the same equation. This is due to the fact that a disc may be regarded as having a large number of rods each with one end at the centre and other at the circumference. But for a ring, there will be no induced emf.

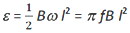
CBSE Electromagnetic Induction ( With Hint / Solution)
Class XII (By Mr. Ashis Kumar Satapathy)
email - [email protected]

Electromagnetic Induction