Solution of Additional Exercises

View Questions

 

Exercise 1

Area of the loop, A = 4 cm x 4 cm = 16 x 10^{- 4} m²
Magnetic field, B = 5 mT = 5 x 10^{- 3} T
Angle, θ = 0⁰
Magnetic flux through the loop, Φ = BA cos θ = 5 x 10^{- 3} x 16 x 10^{- 4} cos 0
= 8 x 10^{- 6} Wb

Exercise 2

Area of the loop, A = 2 cm² = 2 x 10^{- 4} m²
Initial magnetic flux density, B₁ = 0.02 Wb/m²
Final magnetic flux density, B₂ = 0

The induced emf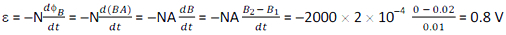

Exercise 3

The potential difference between the ends of the axle of a car is given by ε = B_vvl = 3.0 x 10^{- 5} x 20 x 1.5 = 9.0 x 10^{- 4} V

Exercise 4

The potential difference between the centre and the end of the blade is given by

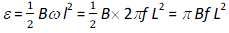
Exercise 5

Peak emf is given by
ε₀ = NBAω
N = 100, B = 0.10 T, A = 10 cm² = 10 x 10^{- 4} m², ω = 100 rad/s
So, ε₀ = NBAω = 100 x 0.10 x 10 x 10^{- 4} x 100 = 1 V
Peak current through the external resistance = ε₀ / (10 + 10) = 1/20 = 0.05 A

Exercise 6

Emf is given by

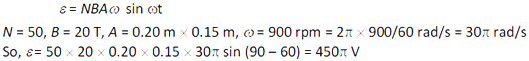
Exercise 7

The coefficient of self-induction of a solenoid is given by

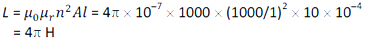
Exercise 8

Emf induced is

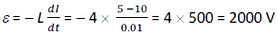
Exercise 9

Flux linkages with the winding are
NΦ = LI
So, the self inductance of the winding is
L = NΦ / I
Enegry stored in the winding is given by
U = ½ LI² = ½ (NΦ / I) I² = ½ NΦI = ½ NΦV/R = ½ x 1000 x 0.01 x 200/20 = 50 J

Exercise 10

The induced emf in the second coil is given by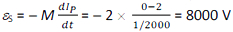

Exercise 11

For co-axial solenoids, the mutual inductance is given by

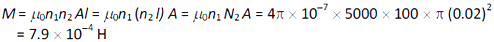
The induced emf in the inner coil is given by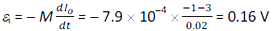

Exercise 12

1. Emf produced = Bvl = 0.3 x 0.01 x 0.08 = 2.4 x 10^{- 4} V
   Induced emf will last for the time in which the loop comes out of the field. In this process it will move a
   distance equal to the length of shorter side. So, time duration
   t = length/speed= 2cm/1cm/s = 2 s


2. Emf produced = Bvl = 0.3 x 0.01 x 0.02 = 0.6 x 10^{- 4} V
   Induced emf will last for the time in which the loop comes out of the field. In this process it will move a
   distance equal to the length of longer side. So, time duration
   t = length/speed= 8cm/1cm/s = 8 s

Exercise 13

The magnetic flux passing through the loop is given by Φ_B = NBA cos ωt = NB πr² cos ωt

The induced emf,

Maximum emf is, ε₀ = NB ωπr² = 20 x 3 x 10^{- 2} x 50 x π (0.08)² = 0.603 V

Average of emf ε = NB ωπr² sin ωt over a cycle is zero.

Maximum induced current is,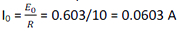

Average power is, Pav = ½ ε₀I₀ = ½ x 0.603 x 0.0603 = 0.018 W

The power dissipated as heat in the coil is supplied by the external mechanism rotating the coil as this mechanism has to do work against the torque produced by induced current which oppose the rotation of the coil.

Exercise 14

Flux linkages with the other coil are
N Φ = MI₁
So, change is flux linkages with the other coil are
Δ (NΦ) = MΔ I₁ = 1.5 x (20 – 0) = 30 Wb

 

CBSE Electromagnetic Induction ( With Hint / Solution)
Class XII (By Mr. Ashis Kumar Satapathy)
email - [email protected]