When the electric current in a coil changes, the magnetic flux linked with that coil also changes.Consequently, an emf is induced in the coil. This type of induction is called self induction and the induced emf is called back emf. The induced emf opposes the change of current according to Lenz's law.
If / is the current flowing in the coil, the flux linked with the circuit is proportional to the current.
That is, φ B ∝ I
For a coil of N turns, the same magnetic flux is linked with all the turns. Therefore, we use the term flux linkage, which is equal to N φ B In this case, the flux linkages
N φ B ∝ I
Nφ B = LI
where L is the selfinductance of the coil. It is also called the coefficient of self-induction.
Inductance is a scalar quantity. The units of self-inductance are henry (H). 1 H = 1 Wb/m. Its dimensions are [M L2 T –2 A–2].
When the current through the coil changes, the flux linked with the coil also changes and an emf is induced in the coil. The induced emf is given by
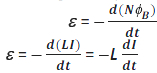
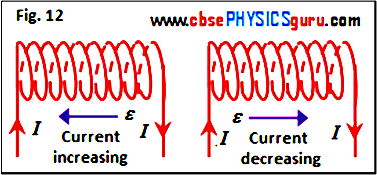
Clearly, the self-induced emf always opposes the change (increase or decrease) of current in the coil. See figure 12.
Self Inductance of a circular coil :
Consider a circular coil of radius r, area A (π r2) and having number of turns N. Let the coil carry
current I. The magnetic field at the centre due to a current I flowing in the coil is given by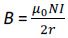
The total flux linked with the coil is given by 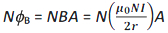
But N φ B = LI. Therefore, the self-inductance of the circular coil is given by 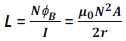

Self Inductance of a long solenoid :
Consider a long air-solenoid of cross sectional area A (π r2), length l and having n number of turns
per unit length. Let the coil carry current I. The magnetic field due to a current I flowing in the solenoid is
given by
B = μ0nI
The total flux linked with the solenoid is given by
NΦB = (nl) (μ0nI) A = μ0 n2 All
But N ΦB = LI. Therefore, the self-inductance of a long solenoid is given by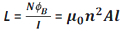
If the interior of the solenoid is filled with a material of relative permeability μr, then the selfinductance
of a long solenoid becomes
L= μr μ0 n2 Al = μ n2 Al
where μ is the (absolute) permeability of the
material filled in the solenoid.
Ferromagnetic materials such as soft iron have a high value of relative permeability. Therefore, the self-inductance of a solenoid increases sharply if it is filled with a ferromagnetic material.
Physical significance of self-inductance :
The self-inductance is the electromagnetic inertia just like mass in mechanics. As we know, work has to be done against inertia to set a particle in motion. Similarly, work has to be done against the back emf in establishing the current through an inductor. This work done is stored as magnetic potential energy (to be discussed later). The effect of self-induction is that the current does not become maximum on making the circuit (i.e. turning the switch on) and does not become zero immediately on breaking the circuit (i. e. turning the switch off).
CBSE Electromagnetic Induction ( With Hint / Solution)
Class XII (By Mr. Ashis Kumar Satapathy)
email - [email protected]
Electromagnetic Induction