Mutual Induction
When the flux produced by a variable current in one coil (usually called primary) links with a closely situated coil (called secondary), there is said to mutual induction.
If I2 is the current flowing in the secondary coil, the flux linkages with the primary coil is proportional to the current in the secondary coil. That is,
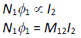
where M12 is the mutual inductance of the primary with respect to the secondary. It is also referred to as the coefficient of mutual induction. Similarly, if I1 is the current flowing in the primary coil, the flux linkages with the secondary coil is proportional to the current in the primary coil. That is,
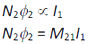
where M21 is the mutual inductance of the secondary with respect to the primary. It is also referred to as the coefficient of mutual induction.
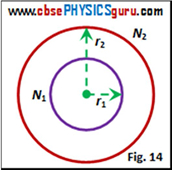
Mutual Inductance of two circular co-axial concentric coils :
Let r1 and r2 (r1 << r2) be radii of two co-axial concentric coils, and N1 and N2 be number of turns in two coils. See figure 14. Let the secondary (outer) coil carry current I2 . The magnetic field at the centre due to a current I2 is given by
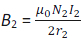
Since the primary (inner) co-axial coil has a very small radius, B2 may be considered constant over the cross-sectional area of the primary. Hence, the total flux linkages with the primary (inner) coil are given by
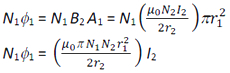
But, N1Φ1 = M12 I2 . Therefore, the mutual-inductance of the of the primary with respect to the secondary is given by
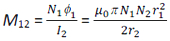
It is not easy to calculate the flux linkage with the secondary (outer) coil as the magnetic field due to the primary (inner) coil varies across the cross section of the secondary coil. Therefore, the calculation of M21 will also be extremely difficult in this case. The equality M12 = M21 = M (say) given by reciprocity theorem is very useful in such situations. Therefore, the mutual-inductance of the of the secondary with respect to the primary is given by
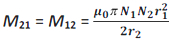
Mutual Inductance of two co-axial solenoids :
Let r1 and r2 be radii of inner (let it be primary P) and outer (let it be secondary S) co-axial solenoids respectively, and n1 and n2 be number of turns per unit length of the two solenoids. Let N1 and N2 be total number of turns in two solenoids and each of length l. See figure 15.
Let the secondary solenoid carry current I2 . This current sets up magnetic flux Φ1 through the primary (inner) solenoid. The total flux linkages with the primary solenoid are given by N1Φ1 = M12 I2
where M12 is the mutual inductance of the primary (inner) solenoid with respect to the secondary (outer) solenoid.
The magnetic field at the centre of the secondary solenoid due to a current I2 is given by B2 = μ0n2I2
The total flux linkages with the primary solenoid are given by
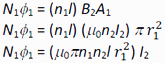
But, N1Φ1 = M12 I2 . Therefore, the mutual-inductance of the of the primary with respect to the secondary is given by
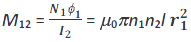
Similarly, the total flux linkages with the secondary solenoid due to current in primary are given by N2Φ2 = (n2l) B1A1
It should be noted here that we are using A1 instead of A2. The flux due to the current I1 in the inner solenoid can be assumed to be confined solely inside this solenoid (i. e. primary) since the solenoids are very long and hence,
N2Φ2 = (n2l) B1A1 (μ0Πn1n2 / r12) / 1
But, N2Φ2= M21 I1. Therefore, the mutual-inductance of the of the secondary with respect to the primary is given by
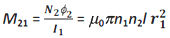
It is clear that M12 = M21 = M (say)
It should be noted here that this equality holds only for long co-axial solenoids. Therefore, for long co-axial solenoids
M = μ0Πn1n2 / r12
It is also important to note that the mutual inductance of a pair of coils, solenoids, etc., depends on their separation as well as their relative orientation.
CBSE Electromagnetic Induction ( With Hint / Solution)
Class XII (By Mr. Ashis Kumar Satapathy)
email - [email protected]
Electromagnetic Induction