SECTION - A
Q. 1. Solve for ![]() and
and 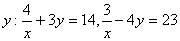
Or
Solve for ![]() and
and 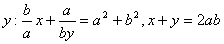
Q. 2. Reduce the following to a rational expression in lowest terms:
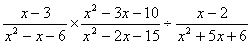
Q. 3. If ![]() is a factor of
is a factor of 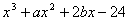 and
and 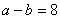 , find the values of a and b.
, find the values of a and b.
Q. 4. If the sum of first n terms of an A.P. is given by Sn = 3n2 + 2n, find the nth term of the A.P.
Or
If m times the m th term of an A.P. is equal to n times its n th term, find its (m + n) th term.
Q. 5. A washing machine is available for Rs. 9,000 cash or Rs. 2,200 as cash down payment followed by 5 monthly instalments of Rs. 1,400 each. Find the rate of interest under the instalment plan.
Q. 6. A loan has to be paid back in two equal annual instalments. If the rate of interest is 16% per annum, compounded annually, and each instalment is Rs. 1,682, find the loan and total interest charged.
Q. 7. Solve for 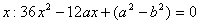
Q. 8. How many terms of the A.P. 3, 5, 7, ..must be taken so that the sum is 120?
Q. 9. Construct a AABC in which AB = 3cm, BC = 4cm and AC = 5 cm. Draw the circumcircle of AABC.
Q. 10. In a right angled triangle ABC, 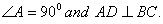 Prove that
Prove that 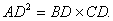
SECTION B
Q. 11. Solve the following system of linear equations graphically: 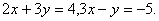
Shade the region bounded by the above lines and the x-axis.
Q. 12. A two-digit number is four times the sum of its digits and is also equal to twice the product of its digits. Find the number.
Q. 13. In Fig. 1, PT' is a tangent and PAB is a secant of the circle. If the bisector of 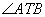 intersects AB at M, prove that PT = PM.
intersects AB at M, prove that PT = PM.
Q. 14. The data about annual production of an Indian State is given below
Commodity |
Wheat |
Sugar |
Rice |
Maize |
Grams |
Annual production (in tones) |
2,750 |
2,500 |
1,500 |
1,000 |
1,250 |
Draw a pie-chart to represent the above data.
Q. 15. If 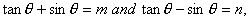 show that
show that 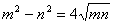
Evaluate: 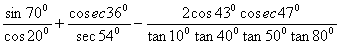
Q. 16. A card is drawn at random from a pack of 52 playing cards. Find the probability that the card drawn is neither an ace nor a king.
Q. 17. The following table gives the distribution of expenditure of different families on education. Find the mean expenditure on education of a family.
Expenditure (in Rs.) |
Number of families |
1000-1500 1500-2000 2000-2500 2500-3000 3000-3500 3500-4000 4000-4500 4500-5000 |
24 40 33 28 30 22 16 7 |
Q. 18. The coordinates of the mid-point of the line joining the points (3p, 4) and (-2, 2q) are (5, p). Find the values of p and q.
Q. 19. Two vertices of a triangle are (1,2) and (3,5). If the centroid of the triangle is at the origin, find the coordinates of the third vertex.
Or
If 'a' is the length of one of the sides of an equilateral triangle ABC, base BC lies on x-axis and vertex B is at the origin, find the coordinates of the vertices of the triangle ABC.
Q. 20. A toy is in the form of a cone mounted on a hemisphere of radius 3.5 cm. The total height of the toy is 15.5 cm. Find the total surface area of the toy. 
SECTION C
Q. 21. The angle of elevation of a cloud from a point 200 m above the lake is 300 and the angle of depression of the reflection of the cloud in the lake is 60°. Find the height of the cloud.
Or
The angle of elevation of a jet plane from a point A on the ground is 60°. After a flight of 15 seconds, the angle of elevation changes to 30°. If the jet plane is flying at a constant height of 1500 ![]() m, find the speed of the jet plane.
m, find the speed of the jet plane.
Q. 22. In a right triangle, prove that the square on the hypotenuse is equal to sum of the squares on the other two sides.
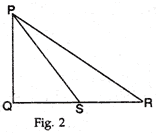
In Fig. 2, PQR is a right triangle, right angled at Q. If QS = SR, show that 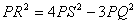 .
.
Q. 23. If a line touches a circle and from the point of contact a chord is drawn, prove that the angles which this chord makes with the given line are equal respectively to the angles formed in the corresponding alternate segments.
Using the above result, prove the following:
If ABC is an isosceles triangle with AB = AC, prove that the tangent at A to the circumcircle of  is parallel to BC.
is parallel to BC.
Q. 24. A hollow cone is cut by a plane parallel to the base and the upper portion is removed. If the curved surface of the remainder is 8/9th of the curved surface of the whole cone, find the ratio of the line segments into which the cone's altitude is divided by the plane.
Or
If the radii of the ends of a bucket, 45 cm high, are 28 cm and 7 cm, find its capacity and surface area.
Q. 25. The annual income of Subhash is Rs. 2,80,000 (exclusive of HRA). He contributes Rs. 6,000 per month towards his provident fund and pays an annual premium of Rs. 8,000 for his LIC policy. If he pays Rs. 3,200 per month towards income tax for the first eleven months of the year, find his income tax liability for the last month of the year.
For calculating income tax, use the following:
| (a) Standard Deduction | |
| Gross income | Deduction |
| (i) Upto Rs.75,000 (ii) From Rs.75,001 to Rs.5,00,000 (iii) More than Rs,5,00,000 Rs.20,000 |
40% of gross income Rs.30,000 Rs.20,000 |
| (b) Rates of Taxes | |
Slab |
Income tax |
| (i) Upto Rs. 50,000 (ii) From Rs. 50,001 to Rs. 60,000 (iii) From Rs. 60,001 to Rs. 1,50,000 (iv) Rs. 1.50,000 and above |
No tax 10% of the amount exceeding Rs.50,000 Rs.1,000+20% of the amount Exceeding Rs.60,000 Rs.19,000+30% of the amount Exceeding Rs.1,50,000 |
| (c) Rebate in Tax | (i) 20% of the savings subject to a maximum of Rs. 14,000 if the gross income is upto Rs. 1,50,000. |