Cyclic Quadrilaeral
Quadrilateral whose all the (four) vertius lie on a circle is called a cyclic quadrilateral.
Theorem 4:- The sum of the either pair of the opposite angle of a cyclic quadrilateral is 1800
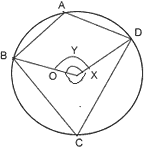
Give: - A cyclic quadrilateral ABCD
To prove:- 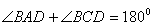
Construction:- Let O be the centre of the circle passing through A, B, C and D. OB and OD are joined.
Proof:- 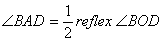
= x/2, say (Theo.2)
and
= y/2, say (Theo.2)
Adding (i) and (ii) we get
As the sum of the angles of a quadrilateral is 3600, there fore,
Example 6. In the adjoining figure, 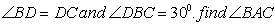
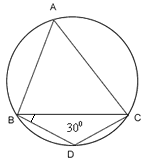
Solution:- As BD = DC
ABCD is a cyclic quadrilateral.
| Subjects | Maths (Part-1) by Mr. M. P. Keshari |
| Chapter 9 | Circle |
| Chapter 10 | Tangents to a circle |
| Chapter 11 | Geometrical Construction |
| Chapter 12 | Troigonometry |
| Chapter 13 | Height and Distance |
| Chapter 14 | Mensuration |
| Chapter 15 | Statistics |
| Chapter 16 | Probability |
| Chapter 17 | Co-ordinate Geometry |