Tangent to a circle is a line which intersects the circle in exactly one point.
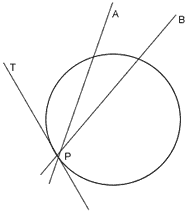
At a point of a circle there is one and only one tangent.
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
The lengths of tangents drawn from an external point to a circle are equal.
Centre of the circle lies on the bisector of the angle between the two tangents.
Theorem 1:- If two chords of a circle intersect inside or outside the circle, then the rectangle formed by the two parts of one chord is equal in area to the rectangle formed by the two parts of the other.
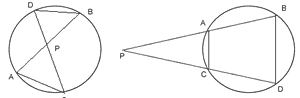
Given:- Two chords AB and CD of a circle such that they intersect each other at a point P lying inside in figure (i) or outside in figure (ii) of the circle.
To prove: - PA.PB = PC.PD
Construction:-AC and BD are joine P.
Proof:-
Case - (1) in figure (i) P lies inside the circle
In
we have
[Angles in jthe same segment]
[vertically opposite angles]
(AA similarity)
Case- (2) In figure (ii) P lies outside the circle
(limear pair)
and
(opposite angles of acyclicq and)
In
[Proved above]
[Common]
(AA similarity)
Hence, in either case,
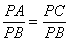
Or, PA.PB = PC.PD
Theorem 2. If PAB is a secant to a circle intersecting it at A and B and PT is a tangent then PA.PB = PT2.
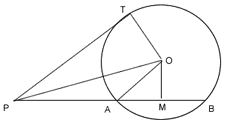
Given: - PAB is secant intersecting the circle with centre O at A and B and a tangent PT at T.
To Prove: - PA.PB = PT2
Construction: - 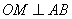 is drawn OA, OP and OT are joined.
is drawn OA, OP and OT are joined.
Proof: - PA = PM – AM
PB = PM + MB
![]()
Also
PM2 = OP2 - OM2 [Pythagoras theo.]
and AM2 = OA2 - OM2 [Pythagoras theo.]
PA.PB = PT2 [Pythagoras theo.]
| Subjects | Maths (Part-1) by Mr. M. P. Keshari |
| Chapter 9 | Circle |
| Chapter 10 | Tangents to a circle |
| Chapter 11 | Geometrical Construction |
| Chapter 12 | Troigonometry |
| Chapter 13 | Height and Distance |
| Chapter 14 | Mensuration |
| Chapter 15 | Statistics |
| Chapter 16 | Probability |
| Chapter 17 | Co-ordinate Geometry |