Equal chords of a circle are equidistant from the centre.
Chords of a circle that are equidistant from the centre are equal.
Theorem 2. The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle.
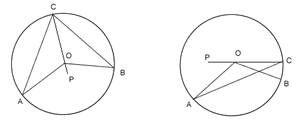
Given: - A circle with centre O and an arc AB subtending 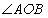 at the centre and
at the centre and 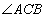 on the remaining part of the circle at C.
on the remaining part of the circle at C.
To prove:- 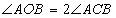
Construction:- CO is joined and produced to P. OA and OB are joined
Proof:- In 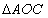
OA = OC (Radii)
[Angle opposite to equal sides]
[Exterior angle of
]
[
]
Similarity, by taking
we have
Adding (i) and (ii) in fig (i) we have
Similarty, subtracting (i) from (ii) in fig. (ii) We have
Note: -
(i) Angle in a semi-circle is a right angle.
(ii) The circle drawn with hypotenuse of a right triangle as diameter pass through its opposite verdes or the arc of a circle subtending a right angle at any point on the remaining part of the circle is a semicircle.
Theorem 3. Angle in the same segment of a circle are equal.
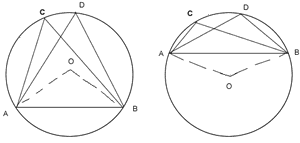
Given:- A circle with centre O and 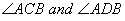 are angles in the same segment.
are angles in the same segment.
To prove:- 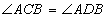
Construction: - OA and OB are joined.
Proof:- In both the figure
from (i) and (ii) we get
Note:- It a line –segment joining two points subtends equal angles at two other points lying on the same side of the line containing the lime-segment, the four points lie on a circle.
Example 3. In the adjoining fig.
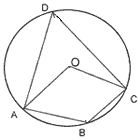
O is centre of the circle and the measure of are ABC is 1000. Determine
.
Solution:- We know that the angle subtended by a chord at the centre of a circle is double the angle subtended at any other point on the circumference in the opposite segment.
Reflex
= 2600
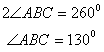
| Subjects | Maths (Part-1) by Mr. M. P. Keshari |
| Chapter 9 | Circle |
| Chapter 10 | Tangents to a circle |
| Chapter 11 | Geometrical Construction |
| Chapter 12 | Troigonometry |
| Chapter 13 | Height and Distance |
| Chapter 14 | Mensuration |
| Chapter 15 | Statistics |
| Chapter 16 | Probability |
| Chapter 17 | Co-ordinate Geometry |