Chapter 9 : Circle

Example 4. Triangle ABC is right angled at B. On the side AC, a point D is taken such that AD = DC and AB = BD. Find the measure of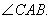

Solution:- The vertices of a right triangle touch a circle with diameter equal to the hypotenuse.

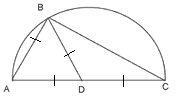
Since AC is the diameter and AD = DC (given)

D is the centre of the circle

AD = DC = BD (radii if the circle given)

But AB = BD (given)

AB = BD = AD --------------------(i)

ABD is an equilateral a triangle

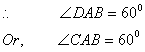
Example 5:- In the adjoining figure, the chord ED is parallel to the diameter AC. Determine .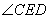

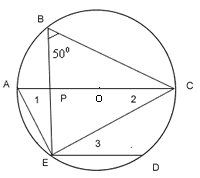
Solution:- 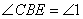[angles in the same segments]

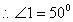
[Angle is the semi-circle]

In

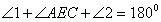
DE || AC                   (given)

               [Alternate interior angles]

Privious Next
Subjects Maths (Part-1) by Mr. M. P. Keshari
Chapter 9 Circle
Chapter 10 Tangents to a circle
Chapter 11 Geometrical Construction
Chapter 12 Troigonometry
Chapter 13 Height and Distance
Chapter 14 Mensuration
Chapter 15 Statistics
Chapter 16 Probability
Chapter 17 Co-ordinate Geometry