Chapter 11 : Geometrical Construction
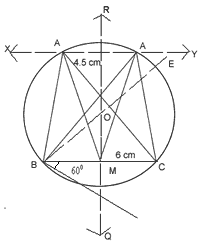
Construction 6. Construct a triangle ABC in which BC = 6cm, 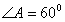 and the attitude through A is 4.5cm. Measure the length of median through A. Write the steps of construction.
and the attitude through A is 4.5cm. Measure the length of median through A. Write the steps of construction.
Procedure:-
- BC = 6cm is drawn and
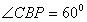 is made downwards with BC of any length.
is made downwards with BC of any length.
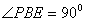 is drawn
is drawn- Perpendicular bisector RQ of BC is drawn which cut BC at M. and intersect BE at O.
- Taking O as centre and OB as radius, a circle is drawn.
- ML = 4.5cm is cut from RQ.
- A line XY, parallel to BC is drawn through L to intersect the circle at A and A'.
AB, AC, A’B and A’C are joined.
ABC and A’BC are the required triangle
Medium AM = A'M = 5.5cm (app.)
Construction 7. Construct a triangle ABC in which BC = 5cm, 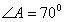 and median AD through A is of length 3.5cm. Also, determine the length of the altitude drawn from A on the side BC (Write the steps of construction also).
and median AD through A is of length 3.5cm. Also, determine the length of the altitude drawn from A on the side BC (Write the steps of construction also).
Procedure:-
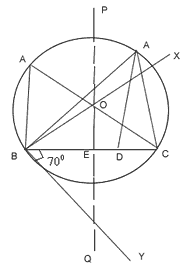
- BC = 5cm is drawn and is constructed downwards.
- BX is drawn perpendicular to BY.
- Q is drawn perpendicular bisector if BC intersecting BX at O and cutting BC at E.
- Taking O as a centre and OB as radius, a circle is drawn.
- Taking E as centre and radius equal to 3.5cm, arc is drawn to cut the circle at A.
- AC and AB are joined
- AD is drawn perpendicular to BC from A to cut BC at D.
- By measuring we find that AD = 3cm.
Construction 8. Construction a 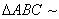 to a equilateral
to a equilateral 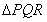 with side 5cm such that each its sides is 6/7th of the corresponding side of
with side 5cm such that each its sides is 6/7th of the corresponding side of 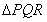 Also draw the circumcircle of
Also draw the circumcircle of 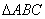 .
.
Procedure:-
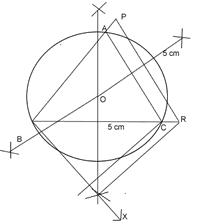
- A ray QX is drawn making any angle with QR and opposite to P.
- Starting from Q, seven equal line segments QQ1, Q1R2, Q2Q3, Q3Q4, Q4Q5, Q5Q6, Q6Q7 are cut of from QX.
- RQ7 is joined and a line CQ6 is drawn parallel to RQ4 to intersect QR at C.
- Line CA is drawn parallel to PR.
ABC is the required triangle.
Construction 9. Construct a triangle ABC in which BC = 6cm, 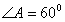 and median AD = 5cm. Also construct another triangle BPQ similar to triangle BCA such that the side BP = 3/2BC.
and median AD = 5cm. Also construct another triangle BPQ similar to triangle BCA such that the side BP = 3/2BC.
Procedure:-
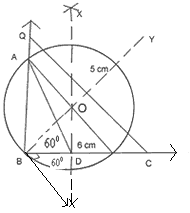
- A line segment BC of length 6cm is drawn.
- At B,
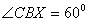 is drawn on downwards.
is drawn on downwards.
- At B,
 is drawn
is drawn
- Perpendicular bisector of BC is drawn which intersect BY at O and BC at D.
- Taking O as a center and OB as a radius a circle passing through B and C is drawn.
- Taking D as a centre and radius 5cm an arc is drawn to intersect the circle at A.
- AB and AC are joined. The required triangle is ABC.
- Taking C as centre and CD as radius an arc is drawn to intersect BC produced at P such that BP = 3/2BC.
- Through P, PQ is drawn parallel to CA meeting BA produced at Q.
- BPQ is the required triangle similar to triangle BCA.
Consyruction 10. Construct a quadrilateral ABCD in which AB = 2.5cm, BC = 3.5cm, AC = 4.2cm, CD = 3.5cm and AD = 2.5cm.
Construct another quadrilateral AB’C’D’ with diagonal AC’ = 6.3cm such that it is similar to quadrilateral ABCD.
Procedure:-
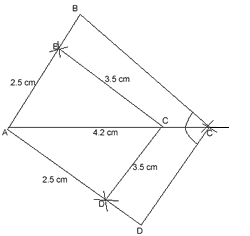
- A line segment Ac = 4.2cm is drawn.
- With A as a centre and radius 2.5cm, two arcs, one above AC and one below AC are drawn.
- With C as centre and radius 3.5cm, two arcs arc drawn intersecting previous arcs at B and D./li>
- AB, AD, BC and CD are joined ABCD is the required quadrilateral.
- Taking A as a centre and radius 6.3cm an arc is drawn to intersect AC produced at C’.
- Through C’, C’B’ and C’D’ are drawn parallel to CB and CD respectively.
AB’C’D’ is the required quadrilateral similar to ABCD.
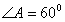 and the attitude through A is 4.5cm. Measure the length of median through A. Write the steps of construction.
and the attitude through A is 4.5cm. Measure the length of median through A. Write the steps of construction.
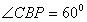 is made downwards with BC of any length.
is made downwards with BC of any length.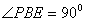 is drawn
is drawn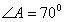 and median AD through A is of length 3.5cm. Also, determine the length of the altitude drawn from A on the side BC (Write the steps of construction also).
and median AD through A is of length 3.5cm. Also, determine the length of the altitude drawn from A on the side BC (Write the steps of construction also).
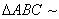 to a equilateral
to a equilateral 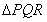 with side 5cm such that each its sides is 6/7th of the corresponding side of
with side 5cm such that each its sides is 6/7th of the corresponding side of 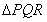 Also draw the circumcircle of
Also draw the circumcircle of ![]() .
.
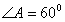 and median AD = 5cm. Also construct another triangle BPQ similar to triangle BCA such that the side BP = 3/2BC.
and median AD = 5cm. Also construct another triangle BPQ similar to triangle BCA such that the side BP = 3/2BC. 
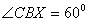 is drawn on downwards.
is drawn on downwards. 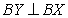 is drawn
is drawn