Exercise - 21
Q. 1. Two circles intersect at A and B. From a point P on one of these circles, two lines segments PAC and PBD are drawn intersecting the other circles at C and D respectively. Prove that CD is parallel to the tangent at P.
Q. 2. Two circles intersect in points P and Q. A secant passing through P intersects the circles at A an B respectively. Tangents to the circles at A and B intersects at T. Prove that A, Q, T and B are concyclic.
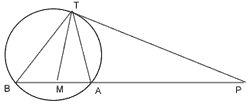
Q. 3. In the given figure. PT is a tangent and PAB is a secant to a circle. If the bisector of 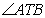 intersect AB in M, Prove that:
(i)
intersect AB in M, Prove that:
(i) 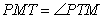 (ii) PT = PM
(ii) PT = PM
Q. 4. In the adjoining figure, ABCD is a cyclic quadrilateral. AC is a diameter of the circle. MN is tangent to the circle at D,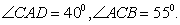 Determine
Determine 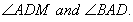
Q. 5. If  is isosceles with AB = AC, Prove that the tangent at A to the circumcircle of
is isosceles with AB = AC, Prove that the tangent at A to the circumcircle of  is parallel to BC.
is parallel to BC.
Q. 6. The diagonals of a parallelo gram ABCD intersect at E. Show that the circumcircles of 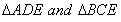 touch each other at E.
touch each other at E.
Q. 7. A circle is drawn with diameter AB interacting the hypotenuse AC of right triangle ABC at the point P. Show that the tangent to the circle at P bisects the side BC.
Answers
| 4. 500, 750 |
| Subjects | Maths (Part-1) by Mr. M. P. Keshari |
| Chapter 9 | Circle |
| Chapter 10 | Tangents to a circle |
| Chapter 11 | Geometrical Construction |
| Chapter 12 | Troigonometry |
| Chapter 13 | Height and Distance |
| Chapter 14 | Mensuration |
| Chapter 15 | Statistics |
| Chapter 16 | Probability |
| Chapter 17 | Co-ordinate Geometry |