If the ratio of the corresponding sides of two similar triangles is 2:3, then what is the ratio of their corresponding height?
The areas of two similar triangles and are 25cm2 and 49 cm2 respectively. If QR = 9.8 cm, find BC.
DE is parallel to BC. If AD = 12.4 cm, DB = 6.2cm, AE = 2x and EC = 6x – 2. Find the value of x.
Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points then the other two sides are divided in the same ratio.
In the given figure, in ABC, DE || BC so that AD = 2.4cm, AE = 32cm and EC=4.8cm. Find AB.
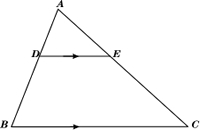
State and prove Basic Proportionality Theorem. Using the above theorem, if ABCD is a trapezium whose diagonals intersect each other at O show that AO/OC = BO/OD.
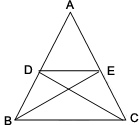
It the given fig-2, if Δ ABE ≅ Δ ACD, prove that ΔADE ~ ΔABC.
Prove that the square of the hypotenuse is equal to the sum of the squares of the other two sides.Using the above result show that sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Prove that the ratio of areas of 2 similar triangles is equal to the ratio of squares of their corresponding sides. Using the above result prove that area of an equilateral triangle described on one side of a square is half the area of triangle described on one of its diagonals.
Find the missing frequencies f1 and f2 in the following frequency distribution table, it is given that the mean of the distribution is 56.
C.I
0 - 20
20 - 40
40 - 60
60 - 80
80 –100
100 - 120
Total
F
16
f1
25
f2
12
10
90
CBSE Important Questions Class X Mathematics By : Mr. Ajai Kumar Shukla
