Exercise - 16
1. In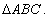 
the bisector of 
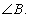intersects the side AC at D. A line parallel to side AC intersects line segment AB, DB and CB at points P, R and Q respectively. Prove that
2. ABCD is a quadrilateral in which AB = AD. The bisector of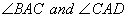 
intersects the side BC and CD respectively at E and F. Prove that the segment EF is parallel to the diagonal BD.
3. In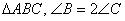 
and the bisector of 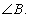intersects AC at D. Prove that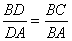 
4. If the diagonal BD of a quadrilateral ABCD bisects both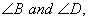 
show that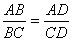 
5. D is the midpoint of side BC of 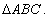DE and DF are respectively bisectors of 
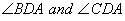such that E and F lie on AB and AC, respectively. Prove that EF || BC.
6. O is a point inside a 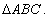The bisector of 
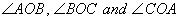meet the sides AB, BC and CA in points D, E and F respectively. Prove that AD. BE. CF = DB. EC. FA
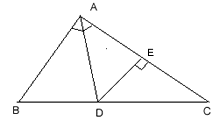
7. In the adjoining figure,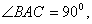 
, AD is bisector of 
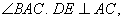Prove that DE X (AB + AC) = AB X AC.
8. If the bisector of an angle of a triangle bisect the opposite side, prove that the triangle is isosceles.
9. BO and CO are respectively the bisectors of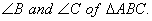 
AO is produced to meets BC at P. Show that
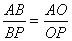
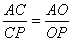
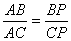
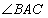
| Subjects | Maths (Part-1) by Mr. M. P. Keshari |
| Chapter 1 | Linear Equations in Two Variables |
| Chapter 2 | HCF and LCM |
| Chapter 3 | Rational Expression |
| Chapter 4 | Quadratic Equations |
| Chapter 5 | Arithmetic Progressions |
| Chapter 6 | Instalments |
| Chapter 7 | Income Tax |
| Chapter 8 | Similar Triangles |
