Chapter 8: Similar Triangles

Example 14. In an equilateral triangle PQR, the side QR is trisected at S. prove that

Solution:-

Given:- In an equilateral 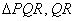is trisected at S.

To Prove:-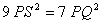

Construction:- is drawn

Proof:- QD = DR = QR/2 ------------(i)

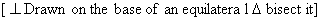
Side QR is trisected at S(given)

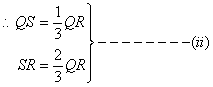
In is acute