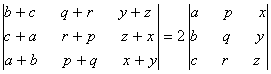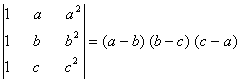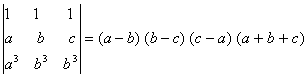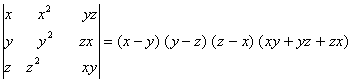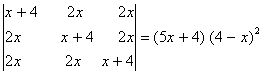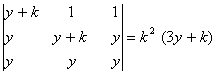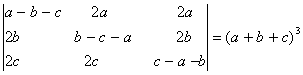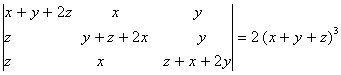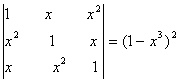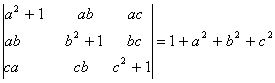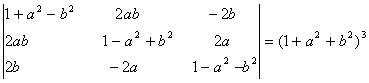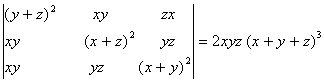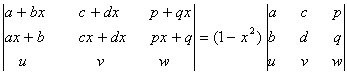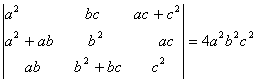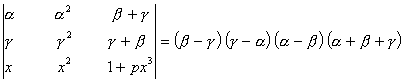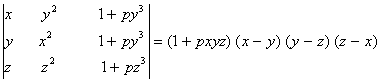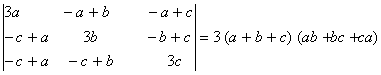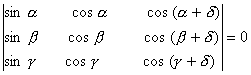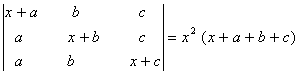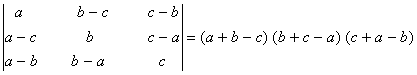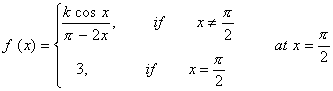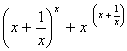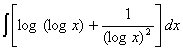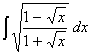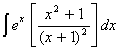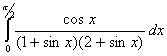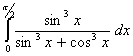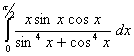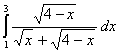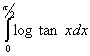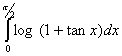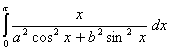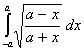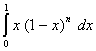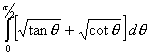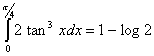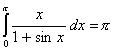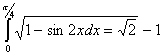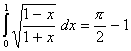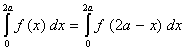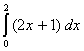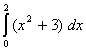CBSE Guess > Papers > Important Questions > Class XII > 2009 > Maths > Mathematics By Mr. Harish Kumar
CBSE CLASS XII
CHAPTER : 1 RELATIONS AND FUNCTIONS
Q. 1. If R is the relation in 
, show that the relation R defined by (a,b)R(c,d) if and only if ad = bc is an equivalence relation.
Q. 2. Let 
be such that fof = f, show that f is onto is and only if f is one to one. Describe f is in this case.
Q. 3. Let R+ be the set of all positive real. Define an operation on 
Q. 4. Define the binary operation '*' on Q as follows 
Find the identity element of (Q,*) .
Q. 5. Let A = Q * Q. Let '*' be the binary operation on A defined by :
(a,b) *.(c,d) =.ac, adb)
Find
- The identity element of (A,*)
- The invertible element of (A,*) .
Q. 6. Consider the binary operation '*' on Q defined by 
i. 
ii. Show that * is not commutative.
iii. Show that ‘*’ is not associative.
Q. 7. Let '*' be the binary operation on N given by a * b -LCM of a and b . Find
- 5 *7 , 20 *16
- Is *commutative
- Is *associative
- Find the identity of * in N
- Which element of N are invertible for?
Q. 8. Let 
and let '*' be the binary operation on A defined by (a,b) * (c,d) = (a +c, b +d) .Show that
i) (A,*) commutative
ii) Find the identity of (A,*) , if any.
Q. 9. Let A be the set of all reals except ‘1’ and ‘0’. '*' be the operation on A defined by a *b -a+ b - ab for 
. Prove that
- A is closed under given operation.
- The given operation is commutative.
- The given operation is associative.
Q. 10. On the set IR - {-1}a binary operation '*' be defined by a *b = a + b +ab 
Prove that '*' is commutative as well as associative on IR - {-1}Find the identity element and prove that every element of IR - {-1}is invertible.
Q. 11. Let 
be a function defined as 
where S is range of f , is invertible. Find the inverse of f .
Q. 12.
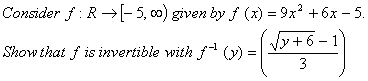
Q. 13.
Q. 14.
- If gof is onto, then g is onto
- If gof is one-one, then f is one-one.
- If gof is onto, and g is one-one, then f is onto.
CHAPTER : 2 INVERSE TRIGONOMETRIC FUNCTIONS
Q. 1. Show that
Q. 2. Solve
Q. 3.
Q. 4.
Q. 5.
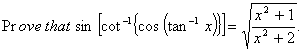
Q. 6.
Q. 7. Find the value of 
CHAPTER : 3 DETERMINANTS
Q. 1. By using the properties of the determinants prove that
Q. 2. If x, y, z are different and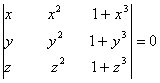 
, then show that 1 + xyz =
Q. 3.
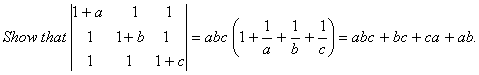
Q. 4. If a,b, c are positive and unequal, show that value of the determinant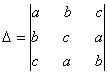 
is negative.
Q. 5.
If a, b, c are reals, and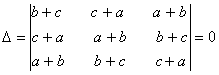 
Show that either a + b + c = 0 or a = b = c.
CHAPTER : 4 CONTINUITY AND DIFFERENTIABILITY
Q. 1. Find all the points of differentiability of f , where f is defined by
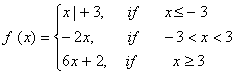
Q. 2. Discuss the continuity of the function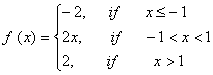 
Q. 3. Find the relationship between a and b so that the function f defined by 
Q. 4. For what values of 
is the function defined by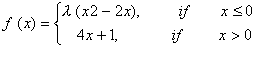 
continuous at x = 0? What about continuity at x = 1?
Q. 5. Find the values of a and b so that the function defined by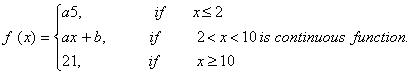 
Q. 6. If the function f (x) given by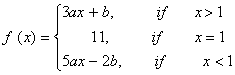 
is continuous at x = 1. Find the values of a and b.
Q. 7. Find the value of k so that the function f is continuous at indicated points:
Q. 8.
Q. 9.
Q. 10. Differentiate W.r.t. x :
Q. 11.
Q. 12.
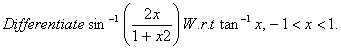
Q. 13.
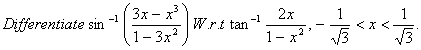
Q. 14.
Q. 15.
Q. 16.
Q. 17.
Q. 18.
Q. 19.
Q. 20.
Q. 21.
Q. 22.
Q. 23.
Q. 24.
Q. 25.
Q. 26. Verify Rolle’s theorem for the function 
Q. 27. Verify Mean value theorem 
Q. 28. Given that for the function f defined by 
Find the value of a and b.
Q. 29. Use Mean Value theorem to find a point on the curve 
defined in the interval [2, 4], where tangent is parallel to the chord joining the end points on curve.
CHAPTER : 5 APPLICATION OF DERIVATIVES
Q. 1. A stone is dropped into a quite lake and waves move in circle at a speed of 4cm per second. At the instant, when the radius of the circular wave is 10cm, how fast is the enclosed area increasing?
Q. 2. The length x of a rectangle is decreasing at the rate of 5cm/minute and the width y is increasing at the rate of 4cm/minute. When x = 8cm and y = 6cm, find the rates of change of a) the perimeter b) the area of the rectangle.
Q. 3. A ladder 5m long is leaning against a wall. The bottom of the ladder is pulled along the ground, away from the wall, at the rate of 2cm/s. How fast is its height on the wall decreasing when the foot of the ladder is 4m away from the wall?
Q. 4. Sand is pouring from a pipe at the rate of 12cm3/s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4cm?
Q. 5. A man of height 2m walks at a uniform speed of 5km/h away from a lamp post which is 6meters high. Find the rate at which the length of his shadow increases.
Q. 6. Find the intervals in which the function f given by 
is strictly increasing or strictly decreasing.
Q. 7. Find the intervals in which following functions are strictly increasing or strictly decreasing:
i. 
ii. 
Q. 8. Find the least value of a such that the function f given by f(x) = x2+ ax + 1 is strictly increasing on (1, 2).
Q. 9. Prove that the function f given by fx = log sin x is strictly increasing on 
Q. 10.
is an increasing function of x throughout its domain.
Q. 11.
Q. 12. Find the point at which the tangent to the curve 
Q. 13. Find the point at which the tangent to the curve 
is parallel to x-axis.
Q. 14. Show that the tangents to the curve 
at the points where x = 2 and x = -2 are parallel.
Q. 15. Find the equation of the normals to the curve 
which are parallel to the line x + 14y + 4= 0.
Q. 16. Find the equations of tangent and normal to the parabola y2 = 4x at the point (at2, 2at)
Q. 17. Prove that the curves x = y2 and xy = kcut at right angles if 8k2 = 1.
Q. 18. Find the equation of the tangent to the curve 
which is parallel to the line 4x - 2y + 5 = 0 .
Q. 19. Show that the curves 
touch each other.
Q. 20. Using differentials find the approximate value of the following :
i. 
ii. 
iii. 
Q. 21. Find the approximate change in the surface area of a cube of side x meters caused by decreasing the side by 1%.
Q. 22. If the radius of a sphere is measured as 7m with an error of 0.02m, then find the approximate error in calculating its volume.
CHAPTER : 6 INTEGRALS
Q. 1. Evaluate:
Q. 2. Evaluate:
Q. 3. Prove that:
Q. 4. Evaluate by limit of sum:
CHAPTER : 7 DIFFERENTIAL EQUATIONS
Q. 1. Form the differential equation corresponding to y2 = a (b - x) by eliminating parameters a and b .
Q. 2. Form the differential equation representing the family of curves y = a sin(x + b) . Where a and b are arbitrary constants.
Q. 3. Form the differential equation representing the family of ellipses having foci on x-axis and centre at origin.
Q. 4. Form the differential equation of the family of curves given by 
, where a is arbitrary constant.
Q. 5. Form the differential equation of family of circles touching the x-axis at origin.
Q. 6. Form the differential equation representing the family of parabolas having vertex at origin and axis along positive direction of x-axis.
Q. 7. Form the differential equation of family of the circles in the second quadrant and touching the co-ordinate axis.
Q. 8. Find the particular solution of the differential equation
, given that y = 1 when x = 0.
Q. 9. Find the particular solution of the differential equation (x - y)(dx + dy) = dx - dy , given that y = -1 when x = 0.
Q. 10. Show that the family of curves for which the slope of the tangent at any point (x, y)on it 
Q. 11. Find the equation of a curve passing through the point (0,1) , if the slope of the tangent to the curve at any point (x, y) is equal to the sum of the x-coordinate and the product of x coordinate and y-coordinate of the point.
Q. 12. Show that the following differential equations are homogeneous and solve each of them:
i. 
ii. 
iii. 
Q. 13. Solve:
i. 
ii. 
iii. 
iv. 
v. 
vi. 
vii. 
viii. 
ix. 
x. 
xi.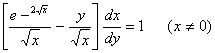 
xii. 
CHAPTER : 8 VECTOR ALGEBRA
Q. 1.
Q. 2. For any two vectors 
, we always have 
Q. 3.
Q. 4. Show that 
is perpendicular to 
for any two non zero vectors .
Q. 5. If 
are unit vectors such that 
, find the value of 
Q. 6. If either vector 
. But converse need not be true. Justify your answer with an example.
Q. 7. Show that the vector, 
form the vertices of a night angled triangle.
Q. 8. Let the vector 
. Then show that 
Q. 9. Let 
, be three vectors such that 
and each one of them being perpendicular to the sum of the other two. Find 
.
Q. 10. Three vectors 
, satisfy the condition 
, Evaluate the quantity 
Q. 11. If with reference to the right handed system of mutually perpendicular unit vectors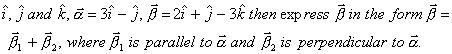 
Q. 12. Show that the points A =(1,-2,-8) , B(5,0,-2) and C(11,3,7) are collinear and find the ratio in which B divides AC.
Q. 13. The two adjacent sides of a parallelogram are 
Find unit vectors parallel to its diagonal. Also find its area.
Q. 14. Let 
. Find a vector 
which is perpendicular to both 
Q. 15. If are mutually perpendicular vectors of equal magnitudes, show that the vector 
Q. 16. Prove that 
, if find only if s are perpendicular. Given 
Q. 17. If 
are unit vectors inclined at an angle , then prove that
i) 
ii. 
Q. 18.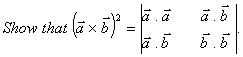 
Q. 19. If are vectors such that 
Q. 20. If are vectors such that 
Q. 21. 
Q. 22. If 
. Then prove that 
where k is a scalar.
Q. 23. Prove that the points A, B and C with position vectors 
respectively are collinear if 
Q. 24. If are three mutually perpendicular vectors of equal magnitude. Prove that the angle which 
makes with any of the vectors 
CHAPTER : 9 THREE DIMENTIONAL GEOMETRY
Q. 1. Show that the lines 
do not intersect.
Q. 2. Find the distance between lines 1 l and 2 l given by
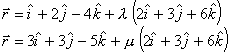
Q. 3. Find the vector equation of the plane passing through the intersection of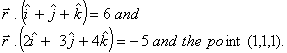 
Q. 4. Find the equation of plane passing through the intersection of the planes 3x - y + 2z - 4 = 0 and x + y + z - 2 = 0 and the point (2,2,1) .
Q. 5. Show that the lines 
are coplanar.
Q. 6. Find the angle between the plane 
Q. 7. Find the equation of the plane passing through the point (- 1,2,1) and perpendicular to the line joining the points (-3,1,2) and(2,3,4) . Find also the perpendicular distance of the origin from this plane.
Q. 8. Find the angle between the two planes 3x - 6y + 2z = 7 and 2x + 2y - 2z = 5 .
CHAPTER : 10 PROBABILITY
Q. 1. In a factory which manufactures bolts, machine A, B and C manufacture respectively 25%, 35% and 40% of the bolts. Of their outputs 5, 4 and 2 percent are respectively defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it is manufactured by machine B?
Q. 2. A man is known to speak truth 3 out of 4 times. He throws a die and reports that it is a six. Find the probability that it us actually six.
Q. 3. An insurance company insured 2000 scooter drivers, 4000 car drivers and 6000 truck drivers. The probability of an accident is 0.01, 0.03 and 0.15 respectively. One of the insured persons meets with an accident. What is the probability that he is a scooter driver?
Q. 4. A card from the pack of 52 cards is lost. From the remaining cards of the pack, two cards are drawn and are found to be both diamonds. Find the probability of lost card being diamond.
Q. 5. A company has two plants to manufacture scooters. Plant I manufacture 70% of the scooters and plant II manufacture 30%. At plant I, 80% of the scooters are rated as of standard quality and at plant II, 90% of the scooters are rated as of standard quality. A
scooter is chosen at random and is found to be of standard quality. What is the probability that it has come from plant II.
Q. 6. There are 3 bags each containing 5 white balls and 3 black balls. Also there are 2 bags each containing 2 white balls and 4 black balls. A white ball is drawn at random. Find the probability that this white ball is from the bag of first group.
Q. 7. In a competitive examination, an examinee either guesses or copies or knows the answer to a multiple choice question with four choices. The probability that he makes a guess is 
and probability that he copies the answer is
. The probability that the answer is correct is, given that he copied it is 
. Find the probability that he knows the answer to the squestion, given that he correctly answered the question.
Q. 8. Find the probability distribution of number of doublets in three throws of a pair of dice.
Q. 9. Let X denotes the number of hours you study during a randomly selected school day. The probability that X can take a value x has the following form, where k is some unknown constant :
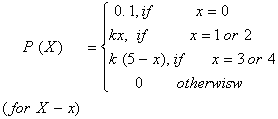
- Find the value of k.
- What is the probability that you study at least two hours? Exactly two hours? At most two hours?
Q. 10. The random variable X has probability distribution P(X) of the following form, where k is some number:
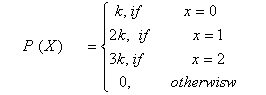
- Find the value of K.
Q. 11. Two cards are drawn simultaneously (or successively without replacement) from a well shuffled pack of 52 cards. Find the mean, variance and standard deviation of the number of kings.
Q. 12. Two dice are thrown simultaneously. If X denotes the number of sixes, find the expectation of X.
Q. 13. Let X denotes the sum of numbers obtained when two fair dice are rolled. Find the variance and standard deviation of X.
Q. 14. In a meeting, 70% of the members favour 30% members oppose a certain proposal. A member is selected at random and we take X = 0 if he opposed, and X = 1 if he is in favour. Find E(X) and Var(X).
Q. 15. Find the probability distribution of number of heads when three coins are tossed. Also find the mean number of heads in the above case.
Q. 16. A pair of dice is thrown 4 times. If getting a doublet is considered a success. Find the probability of two successes.
Q. 17. There are 5% defective items in a large bulk of items. What is probability that a sample of 10 items will not include more than one defective item.
Q. 18. A fair coin is tossed 10 times. Find the probability of
- Exactly six heads.
- At least six heads
- At most six heads.
Q. 19. Find the mean of binomial distribution 
Q. 20. Five dice are thrown simultaneously. If the occurrence of an even number in a single dice is considered a success. Find the probability of getting at most 3 successes.
Q. 21. An unbiased dice is thrown three times. Getting 3 or 5 is considered as success. Find the probability of at least two successes.
Q. 22. An urn contains seven white, 5 black and 3 red balls. Two balls are drawn at random.
Find the probability that :
- Both the balls are red.
- One ball is red and other is black.
- One ball is white.
Q. 23. 3 cards are drawn at random from a pack of well shuffled 52 cards. Find the probability that :
- All the three cards are of same suit.
- One is a king; the other is a queen and third is a jack.
Q. 24. There are two bags I and II. Bag I contains 3 white and 2 red balls, bag II contains2 white and 4 red balls. A ball is transferred from bag I to bag II (without seeing its colour) and then ball is drawn from bag II. Find the probability of getting a red ball.
Q. 25. Bag I contains 3 red and 4 black balls and bag II contains 4 red and 5 black balls. One ball is transferred from bag I to bag II and then a ball is drawn from bag II. The ball so drawn is found to be red in colour. Find the probability that the transferred ball is black.
ANSWERS
CHAPTER : 1 RELATIONS AND FUNCTIONS
1. f is identity function.
3. 
4. 0
5. 
6. 
7.i 35, 80
ii. yes
iii. yes
iv. 1
v. 1
8. Identity does not exist
10. 0
11. 
12. 
CHAPTER : 2 INVERSE TRIGONOMETRIC FUNCTIONS
2.i. 
ii.
iii. 
3. 
7. 
CHAPTER : 4 CONTINUITY AND DIFFERENTIABILITY
1. x = 3
2. continuous
3. 
4. 
5. a = 2, b = 1
6. a = 3, b = 2
7.i. k = 6
ii. 
8. 
9.i. 
ii.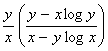 
iii. 
iv. 
10.i. 
ii.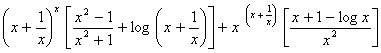 
iii. 
iv. 
v. 
vi. 
s
12. 2
13. 
14. 
15. 
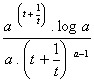
24. 
28. a = 11, b= -6
29. 
CHAPTER : 5 APPLICATION OF DERIVATIVES
1. 
2. 
3. 
4. 
5. 
6. Strictly increasing in 
, strictly decreasing in 
7.a. Strictly increasing in (-2, -1), strictly decreasing in 
b. Strictly increasing in 
, strictly decreasing in 
8. -2
12. (3, 2)
13. (3, - 20), (-1,12)
15. x + 14y – 254 = 0, x + 14y + 86 = 0
16. x = ty – at2, y = -tx + 2at + at3
18. 48x – 24y = 23
20.i. 7.035
ii. 0.008
iii. 
21. 0.12x2 m2
22. 
CHAPTER : 6 INTEGRALS
1. i.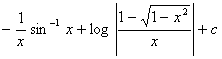 
ii. 
iii. 
iv.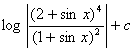 
v. 
vi.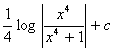 
vii.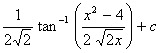 
viii. 
ix.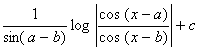 
x. 
xi. 
xii.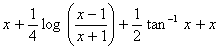 
xiii. 
xiv. 
xv. 
xvi.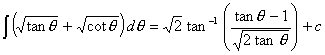 
xvii.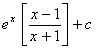 
xviii.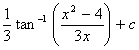 
2.i. 
ii. 
iii. 
iv. 1
v. 0
vi. 
vii. 
viii. 
ix. 
x. 
xi. 
3.i. 6
ii. 
iii. 
iv. 
v. 
CHAPTER : 7 DIFFERENTIAL EQUATIONS
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. x + y = log (x - y) - 1
12.i x2 + y2 = cx
ii. 
iii. 
13.i. 
ii. 
iii. 
iv. 
v. 
vi. 
vii. 
viii. 
ix. 
x. 
xi. 
xii. y (secx + tanx) = (secx + tanx – x) + c
CHAPTER : 8 VECTOR ALGEBRA
1. 
3. 
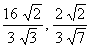
5. 
9. 
10. 
11. 
12. 2 : 3
13. 
14. 
CHAPTER : 9 THREE DIMENTIONAL GEOMETRY
1. 
3. 
4. 7x – 5y + 4z – 8 = 0
5. 
7. 
8. 
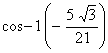
CHAPTER : 10 PROBABILITY
1. 
2. 
3. 
4.
5. 
6. 
7. 
8.
| x | 0 |
1 |
2 | 3 |
P (X) |
|
|
 |
 |
9a. k = 0.15
9b. 0.75,0.3, 0.55
10. 
11.a. 
11.b. 
12.
13. Var (X) = 5.833, S.D = 2.415
14. E (X) = 0.7 and Var (X) = 0.21
15.
| x | 0 |
1 |
2 | 3 |
P (X) |
|
|
|
|
, 
16. 
17. 
18.i. 
ii. 
iii. 
19. 
20. 
21. 
22.i. 
ii. 
iii. 
23.i. 
ii. 
24. 
25. 
Paper By Harish Kumar PGT Mathematics , JNV Jalandhar, Ph No. 09463647493
