CBSE Guess > Papers > Important Questions > Class XI > 2010 > Maths > Maths By Mr. Anil Kumar Tondak

CBSE CLASS XI

Sequences & Series

Q.1. The sums of n terms of two arithmetic progressions are in the ratio 5n + 4 : 9n +6. Find the ratio of their 18th terms.

Q.2. Show that the sum of (m + n)th and (m – n)th terms of an A.P. is equal to twice the mth term.

Q.3. If an=n2+3n. Find Sn.

Q.4. The sum of n terms of two arithmetic progressions are in the ratio (3n + 8) : (7n + 15). Find the ratio of their 12th terms.

Q.5. The ratio of the sums of n terms of two A.P is (7n +1) : (4n +27).find the ratio of their 11th terms.

Q.6. The ratio of the sums of n terms of two A.P is (3n +4): (5n+6 ).find the ratio of their 5 th terms.

Q.7. There are n A.M between 1 and 23 such thart the ratio of last mean to the first mean is 7:1. find the value of n.

Q.8. AM.s have been inserted between 1 and 31 so that the ratio of 7th and (n-1)th means is 5:9. find the value of n

Q.9. Find two numbers whose AM=34 and GM=16

Q.10. The AM of two positive numbers a and b (a>b)is twice the GM Prove that a:b =2 +√3 : 2-√3

Q.11. For the what value of n ,(a n-1 + b n-1) / (a n +b n )is GM of a and b .?

Q.12. Construct a quadriatic equation in x so that AM of its root is Aand GM is G.

Q.13. Find the sum of integers from 1 to 100 that are divisible by 2 or 5.

Q.14. The sums of n terms of two arithmetic progressions are in the ratio 5n + 4 : 9n + 6. Find the ratio of their 18th terms.

Q.15. If a , b, c are in AP . prove that b+c , c+a, a+b are in AP.

Q.16. If a , b, c are in AP. Prove that 1/bc, 1/ac,1/ab are also in AP.

Q.17. If a , b, c are in AP.prove that 1/( √b + √c),1/ (√c +√a),1/( √a + √b) are in AP.

Q.18. If a , b, c are in AP.prove that a2(b +c), b2(c +a), c2 (a+b) are in AP.

Q.19. If a , b, c are in AP. Prove that (b+c)2- a 2,(c+a)2 -b2,(a+b)2-c2 are in AP.

Q.20. If a , b, c are in AP .prove that a(b+c)/bc, b(c+a)/ca, c(a+b)/ab are in AP.

Q.21. If a , b, c are in AP prove that b+c-a, c+a-b,a+b-c .are in AP.

Q.22. If a , b, c are in AP.prove that bc-a2,ca-b2,ab-c2 are in AP.

Q.23. If a2,b2,c2 are in AP.then show that 1/(b+c),1/(c+a),1/(a+b) are in AP.

Q. 24. If a2,b2,c2 are in AP.then show that a/b+c,b/c+a,c/a+b.are in AP.

Q.25. If (b+c-a)/a,(c+a-b)/b,(a+b-c)/c are in AP.prove that 1/a,1/b,1/c are also in AP.

Q.26. Find the sum of the series 12 + 42 + 72 +….

Q.27. Find the sum of the series 2 + 11 + 101 + 1001 + ............. To n terms.

Q.28. Find the least n for which the sum of the series 1 + 2 + 4 + 8 + ........... is greater than 10000.

Q.29. Find the sum of the sequence 8, 88, 888, 8888,------- to n terms.

Q.30. Find the sum of 0.7 + 0.77 + 0.777 + ------- to n terms.

Q.31. The sum of 4 numbers in GP is 40 and arithemetic mean of first and last is 18 .find the numbers.

Q.32. The AM of two numbers exceeds the GM by 8 and ratio of the numbers is 4 .find the numbers.
Q.33. Find the value of n so that 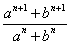may be the geometric mean between a and b.

Q.34. The sum of two numbers is 6 times their geometric means, show that numbers are in the ratio of .

Q.35. Find the sum to n terms of the series: 1 + 5 + 12 + 22 + 35 + - - -

Q.36. Find the sum to n terms of the series : 3 ´ 12 + 5 ´ 22 + 7 ´ 32 +------------
Q.37. If a,b,c are in GP.and then show that x, y, z are in AP

Q.38. If p,q,r are in AP.show that pth,qth,and rth terms of any GP are in GP.

Q.39. If pth , qth and rth terms of a G.P. are a, b and c respectively. Prove that aq-r br-p cp-q =1.

Q.40. If S1, S2, S3 are the sums of first n natural numbers, their squares and their cubes respectively, show that 9 S22 = S3 (1 + 8S1).

Q.41. Sum of the first p, q and r terms of an A.P. are a, b and c respectively. Prove that

Q.42. If the coefficient of ar - 1, ar and ar + 1 in the expansion of (1 + a)n are in arithmetic progression, prove that n2 - n(4r + 1) + 4r2 - 2 = 0.

Q.43. One side of a square is 10cm. The mid points of its sides are joined to form another square whose midpoints are again joined to form one more square and this process is continued indefinitely.find the sum of the areas of all the squares so formed.

Q44. A ball is dropped from a height of 48 m and rebounds two- third of the distance it falls .if it continues to fall and rebounds in this way how far it travels before coming to rest.

Q.45. One side of an equilateral triangle is 12 m .the midpoints of its sides are joined to form another triangle whose midpoints in turn are joined to form still another triangle. This process is continued till 6 triangles are formed.Find sum of perimeters of all the triangles.

Q46. If S be the sum, P be the product and R be the sum of the reciprocals of n terms of a GP, show that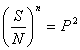

Paper By Mr. Anil Kumar Tondak
Email Id : [email protected]
Ph No.: 9811363962