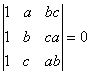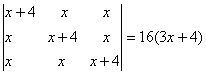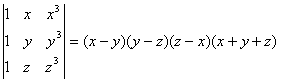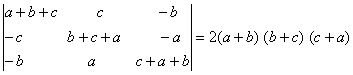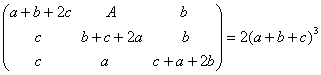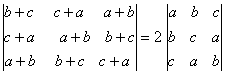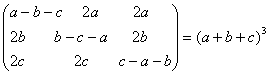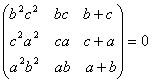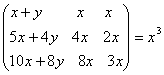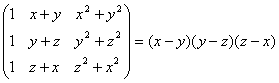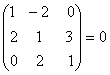CBSE Guess > Papers > Important Questions > Class XII > 2007 > Maths > Matrices Determinants By Mr. V. Nagarajan
Matrices Determinants
O. 1.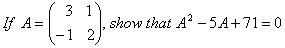
O. 2.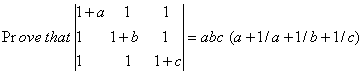
O. 3. Solve the following system of equations by Cramer’s rule:
2x + 3y = 10, x + 6y = 4.
O. 4.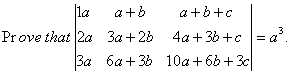 
O. 5.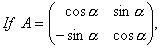
then verify that A . A’ = I.
O. 6.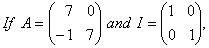
then find k so that: A2 = 8A + kI.
O. 7. Without expanding the determinant show that a+b+c is a factor of the determinant 
O. 8. Solve the following system of equations by Cramer’s rule:
x - 2y = 4, -3x + 5y + 7 = 0.
O. 9.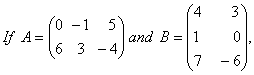 
show that (AB)’ = B’A’.
O. 10. Without expanding the determinant, prove that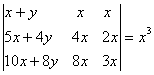 
O. 11.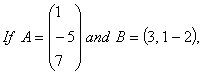
verify that (AB)’ = B’A’.
O. 12. Find a 2x2 matrix, B such that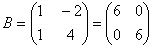 
O. 13. Construct a 2x2 matrix a = [aij], whose elements are given by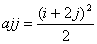 
O. 14. Using determinants, find the area of the triangle whose vertices are (-2,4), (2,-6) and (5,4 ). Are the given points collinear?
O. 15. Define a symmetric matrix. Prove that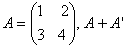 
for is a symmetric matrix where A’ is transpose of A.
O. 16. Using determinants, find the area of the triangle with vertices (-3, 5) (3,-6) & (7,2).
O. 17. Express the matrix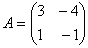 
as the sum of the symmetric and skew - symmetric matrix.
O. 18. Compute the adjoint of the matrix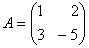 
and verify that A.(adj A)= |A| I.
Q. 19. For matrix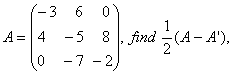 
where A’ is the transpose of the matrix A.
O. 20.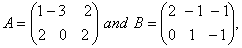
find a matrix C such that A + B+C is a zero matrix.
O. 21. Construct a 2 X 3 matrix whose elements in the ith row and jth column are given by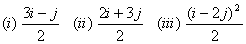 
O. 22. Without expanding the determinant, prove that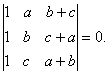 
O. 23. If f(x) x²-4x+1, find f(A) when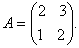 
O. 24. Without expanding the determinant, prove that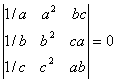 
O. 25. Find a matrix X such that 2A+ B+ X = 0, where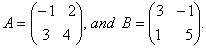 
O. 26.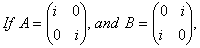
show that AB¹ BA.
O. 27.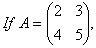
prove that A – AT is a skew symmetric where AT denotes the transpose of A.
Q. 28.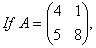 
prove that A + AT is a skew symmetric where AT denotes the transpose of A.
O. 29.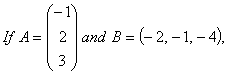
verify that (AB)’ = B’A’.
O. 30. From the following equation, find the values of x and y:
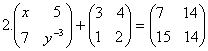
O. 31. Using properties of determinants,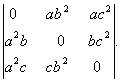 
O. 32. Using properties of determinants show that
i.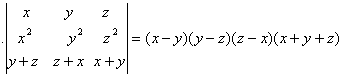 
ii.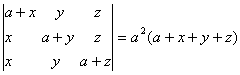 
O. 33. Find X such that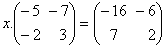 
O. 34. Solve by crammer’s rule: 5x-7y+z = 11, 6x-8y-z = 15, 3x+2y –6z =7.
O. 35. Show that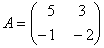 
satisfies the equation x2 -3x - 7 = 0. Thus, find A-1.
O. 36. Using properties of determinants show that:
O. 37.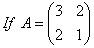
verify A2- 4A - I = 0 where 
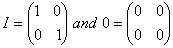hence find A-1.
O. 38. Using cramer’s rule solve the following system of equations: 3x - 2y = 5, x - 3y + 3 = 0.
O. 39. Using properties of determinants show that:
O. 40. Solve the following system of equations by matrix method:
i. 3x + 4y + 7z = 14, 2x - y + 3z = 4, x + 2y – 3z = 0
ii. 2x - z = 3, 5x + y = 7, y + 3z = -1
iii. x + 2y - 3z = 6, 3x + 2y - 2z = 3,2x - y+ z = 2.
iv. x + y + z =1,x - 2y + 3z =2, x - 3y + 5z =3
v. x - y + z =3, 2x + y - z=2, -x - 2y + 2z= -1.
vi. x + y + z = 6, x + 2y + 3z =14, x + 4y + 7z =30
vii. x + 2y - 3z = -4, 2x + 3y + 2z = 2, 3x - 3y - 4z = 11
viii. 5x + 3y + z = 16, 2x + y + 3z = 19, x + 2y + 4z = 25
ix. 2x + 6y =2, 3x - z= -8, 2x – y + z + 3= 0.
x. 2/x + 3/y +10/z = 4, 4/x – 6/y +5/z = 1, 6/x + 9/y – 20/z = 2
xi) 6x-12y+25z = 4, 4x+15y-20z= 3, 2x+18y+15z = 10xii. x+2y+z=7, x+3z=11, 2x-3y=1
O. 41.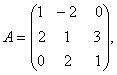 
If find A-1. Using A-1, solve the following system of equations: x - 2y = 10, 2x + y + 3z = 8, -2y + z = 7.
O. 42.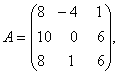 
If find A-1. Using A-1, solve the following system of equations: 8x-4y+z=5, 10x + 6z =4, 8x + y + 6z = 5/2
O. 43.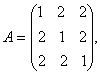 
If find A-1 and hence prove that: A2- 4A –5I = 0.
O. 44.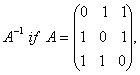 
Find Also, show that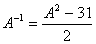 
O. 45.F ind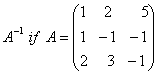
Hence, find the following system of equations: x+2y+5z=10, x-y-+2 = 0, 2x + 3y - z + 11 =0.
O. 46.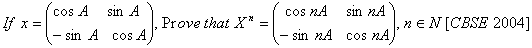 
O. 47. Using properties of determinants, prove that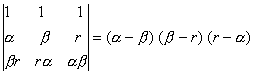 
O. 48. Using matrix method solve the following system of linear equations: x + y - z = 1, 3x + y -2z = 3, x - y - z = -1 [CBSE 2004]
O. 49.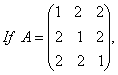
prove that A2; - 4A – 5I = 0. [CBSE 2004]
O. 50. Using properties of dets/. prove that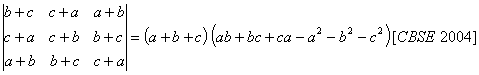 
O. 51.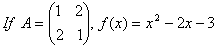 
show that f(A)= 0. [CBSE 05]
O. 52. Using properties of determinants, solve for x: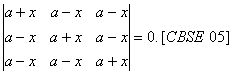 
O. 53. Using matrix method solve the following system of linear equations: x + y - z = 1, x - y – z = -1, 3x + y-2z = 3. [CBSE 05]
O. 54.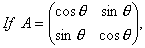 
then prove by principle of Mathematical induction that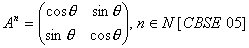 
O. 55. Using matrix method solve the following system of linear equations: x+2y+z = 7, x+3z = 11, 2x - 3y = 1. [CBSE 05]
O. 56. Find the value of x,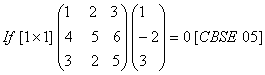 
O. 57. Express the matrix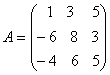 
as the sum o a symmetric and the skew symmetric matrix. [CBSE 2006]
O. 58. Using properties of determinants, prove the following: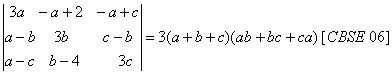 
O. 59. Using matrices, solve the following system of equations
3x - y + z = 5, 2x - 2y + 3z = 7, x + y - z = -1. [CBSE 2006]
O. 60.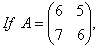 
show that A2 – 12A + I = 0. Hence find A-1. [CBSE 06]
O. 61. If a, b and c are in A.P. show the following: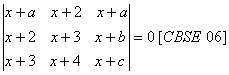
O. 62. Using matrices, solve the following system of equations
x + 2y - 3z = 6, 3x + 2y - 2z = 3, 2x – y + z = 2. [CBSE 2006]
O. 63.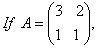 
find the values of a and b such that A2 + Aa + b = 0. hence find A-1. [CBSE 06].
O. 64. Using properties of determinats, prove the following: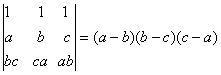 
[CBSE 06]
O. 65. Using matrices, solve the following system of equations.
2x - y + z = 0, x + y - z = 6, 3x – y – 4z = 7. [CBSE 06]
