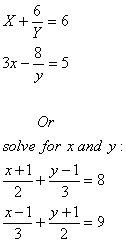CBSE Guess > Papers > Question Papers > Class XII > 2007 > Mathematics > Delhi Set - III
Mathematics — 2007 (Set III — Delhi)
Section- A
Question numbers 1 to 7 carry 2 marks each.
Qs. 1. lf x - p is the GCD of x2 + x - 12 and 2x2 – 3x – 9, find the value of p.
Qs. 2. P and Q are points on sides CA and CB respectively of right angled at C.
Prove that
AQ2 + BP2 = AB2 + PQ2
Or
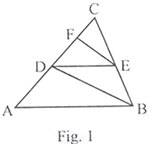
In Fig.1, DE II AB and FE II DB. Prove that DC2 = CF. AC
Qs. 3. Find the sum of first 32 terms of an A.P. whose nth term is 5 - 2n.
Qs. 4. A washing machine is available for Rs.13, 500 cash or Rs. 6,500 as cash down payment followed by three monthly instalments of Rs.2, 500 each. Find the rate of interest charged under instalment plan.
Qs. 5. Solve for x and y:
Qs. 6. Cards marked with numbers 3, 4, 5........, 50 are placed in a box and mixed thoroughly. One card is drawn at random from the box. Find the probability that number on the drawn card is.
- Divisible by 7.
- a number which is a perfect square.
Qs. 7. The mean of the following frequency distribution is 62.8. Find the missing frequency x.
| Class | 0 - 20 | 20 - 40 | 40 - 60 | 60 - 80 | 80 - 100 | 100 - 120 |
| Frequency | 5 | 8 | X | 12 | 4 | 8 |
Section- B
Question numbers 8 to 19 are of 3 marks each.
Qs. 8. Solve the following system of equations graphically.
2x + 3y = 2; x - 2y = 8
Qs. 9. Simplify:
Qs. 10. A man borrows money from a finance company and has to pay it back in two equal half-yearly instalments of Rs. 7,396 each. If the interest is charged by the finance company at the rate of 15% per annum, compounded semi-annually, find the principal and the total interest paid.
Qs. 11. Show that the points (7, 10), (-2, 5) and (3, - 4) are the vertices of an isosceles right triangle.
Qs. 12. Draw a with base QR = 6 cm, vertical angle P = 600 and median through P to the base is of length 4.5 cm.
Qs. 13. Prove that
or
Evaluate without using trigonometric tables:
Qs. 14. Which term of the A.P. 3, 15, 27, 39...... Will be 132 more than its 60th term?
Qs. 15. A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball from the bag is four times that of a red ball, find the number of blue balls in the bag.
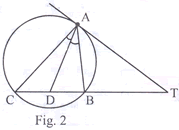
Qs. 16. In Fig. 2, TA is a tangent to the circle from a point T and TBC is a secant to the circle. If AD is the bisector of ![]() prove that
prove that ![]() is isosceles.
is isosceles.
In ![]() , AD
, AD ![]() BC and AD2 = BD.DC. Prove that
BC and AD2 = BD.DC. Prove that ![]() is a right angle.
is a right angle.
Qs. 17. A toy is in the form of a cone mounted on a hemisphere of common base radius 7 cm. The total height of the toy is 3 1 cm. Find the total surface area of the toy.
Qs. 18. Find the ratio in which the point (- 3, k) divides the line segment joining the points (- 5, - 4) and (- 2, 3). Hence find the value of k.
Qs. 19. The enrolment of a secondary school in different classes is given below:
| Class | VI | VII | VIII | IX | X |
| Enrolment | 800 | 500 | 400 | 700 | 200 |
Draw a pie chart to represent the above data.
Section- C
Question numbers 20 to 25 carry 5 marks each.
Qs. 20. A sphere, of diameter 12 cm, is dropped in a right circular cylindrical vessel, partly filled with water. If the sphere is completely submerged in water, the water level in the cylindrical vessel rises by ![]() cm. Find the diameter of the cylindrical vessel.
cm. Find the diameter of the cylindrical vessel.
Or
A solid right circular cone of diameter 14 cm and height 8 cm is melted to form a hollow sphere. If the external diameter of the sphere is 10 cm, find the internal diameter of the sphere.
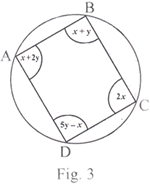
Qs. 21. Prove that the sum of either pair of opposite angles of a cyclic quadrilateral is 180°. Using the above, find x and y in Fig. 3.
Qs. 22. A passenger train takes 2 hours less for a journey of 300 km, if its speed is increased5 km/hour from its usual speed. Find its usual speed.
Or
By increasing the list price of a book by Rs. 10, a person can buy 10 books less for Rs. 1,200. Find the original list price of the book.
Qs. 23. A boy standing on a horizontal plane finds a bird flying at a distance of 100 m from him at an elevation of 300. A girl standing on the roof of 20 metre high building, finds the angle of elevation of the same bird to be 45°. Both the boy and the girl are on opposite sides of the bird. Find the distance of bird from the girl.
Qs. 24. If a line is drawn parallel to one side of a triangle, to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
Using the above, prove the following:
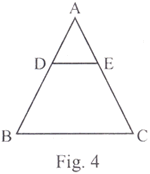
In Fig. 4, DE I I BC and BD = CE. Prove that ABC is an isosceles triangle.
Qs. 24. Ms. Shahnaz earns Rs. 35,000 per month (excluding HRA). She donates Rs. 30,000 to Prime Minister Relief Fund (100% exemption) and Rs. 40,000 to a Charitable Hospital (50% exemption). She contributes Rs. 5,000 per month to Provident Fund and Rs. 25,000 per annum towards LIC premium. She purchases NSC worth Rs. 20,000. She pays Rs. 2,300 per month towards income tax for 11 month. Find the amount of income tax she has to pay in 12 month of the year.
Use the following to calculate income tax:
| a. Saving: | 100% exemption for permissible saving upto Rs. 1, 00,000. |
| b. Rates of income tax for ladies | |
| Slab | Income tax |
| Upto Rs. 1,35,000 | No tax |
| From Rs. 1,35,001 to Rs. 1,50,000 | 10% of taxable income Exceeding Rs. 1, 35,000 |
| From Rs. 1,50,00 1 to Rs. 2,50,000 | Rs. 1,500 + 20% of the amount Exceeding Rs. 1, 50,000 |
| Rs.2,50,00landabove | Rs. 21,500 + 30% of the amount exceeding Rs. 2, 50,000 |
| c. Education Cess: | 2% of income tax payable |
| Mathematics 2007 Question Papers Class XII | |||||
| Delhi | |||||
| Set I | Set III | ||||