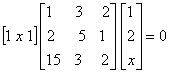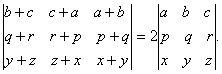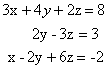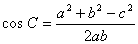CBSE Guess > Papers > Question Papers > Class XII > 2006 > Mathematics > Compartment Delhi Set - I.
Mathematics — 2006 (Set I — Compartment Delhi)
SECTION - A
Q. 1. Find the value of x if
Q. 2. Using properties of determinants, prove the following:
Q. 3. Two unbiased dice are tossed simultaneously. Find the probability that the sum of the numbers will be a multiple of 3 or 5.
Q. 4. There are two bags. The first bag contains 4 white and 2 black balls, while the second bag contains 3 white and 4 black balls. A bag is picked up at random and a ball is drawn out. Find the probability that it is a white ball.
Q. 5.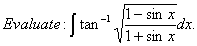 
Q. 6.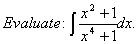 
Q. 7. Solve the differential equation:
given that y = 0 when x = 1.
Q. 8. Solve the differential equation:
Or
Solve the differential equation:
Q. 9. For each x in Boolean algebra B, show
Or
Simplify the following switching circuit by using the Boolean algebra:
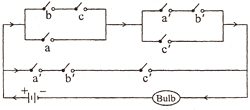
Q. 10.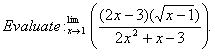 
Q. 11. Differentiate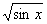 
w.r.t.x from first principle.
Q. 12. Differentiate the following w.r.t. x: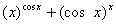 
Q. 13. A point source of light along a straight road is at a height of ‘a’ metres. A boy ‘b’ metres in height is walking along the road. How fast is his shadow increasing if he is walking away from the light at the rate of c metres per minute?
Q. 14.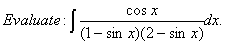 
Q. 15.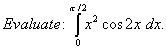 
Or
Using properties of definite integrals, evaluate the following:
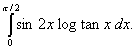
Q. 16. Using matrices, solve the following sys tem of linear equations:
Q. 17. Find the largest possible area of the right-angled triangle whose hypotenuse is 5 cm.
Or
Prove that the radius of the right circular cylinder of the greatest curved surface that can be inscribed in a given cone is half of the radius of the cone.
Q. 18. Using integration, find the area of the region enclosed between two circles x2 + y2 = 1and ` (x - 1)2 + y2 = 1.
Or
Using integration, find the area bounded by the curve x2 = 4y and the straight line x = 4y – 2.
SECTION - B
Q. 19. If a, b and c are the length of sides opposite to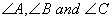 
respectively of then show that
Q. 20. Using vectors, prove that if two medians of a triangle ABC be equal, then it is an isosceles triangle.
Q. 21. The displacement s of a particle at a time t is given by s = 2t3 — 5t2 + 4t — 3. Find
- the time when its acceleration will be 14 m/sec2, and
- the displacement of the particle at that time.
Q. 22. A boy throws a ball vertically upwards from the ground to touch the top of a pole and fall down. If the ball falls down on the ground in just 4 seconds, find the height of the pole. (Use g = 10 m/sec2)
Or
A bullet is projected with a velocity 200 rn/sec at an angle of 60° with the horizontal. Find
- the greatest height attained, and
- the horizontal range covered by it.
(Take g = 10 rn/sec2)
Q. 23. Find the foot of the prependicular drawn from the point P (1, 6, 3) on the line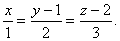 
Also find its distance from P.
Q. 24. The resultant of two forces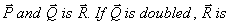 
doubled. If the direction of 
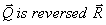is again doubled. Find the ratio between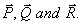 
Or
The resultant of two forces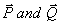 
is of magnitude 
is doubled, the magnitude of the resultant will be and it will be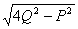 
at right angles to .
Q. 25. Three forces are in equilibrium. The angle between the first and the second is 1200, between the second and the third is 135°. Find the ratio between their magnitudes.
Q. 26. Find the radius of the circular section of the sphere x2 + y2 + z2 - 2y - 4z - 20 = 0 by the plane x + 2y + 2z = 15.
SECTION - C
Q. 19. An urn contains 5 white and 3 red balls. Find the probability distribution of the number of red balls, with replacements, in three draws.
Q. 20. Suppose 8% of people in a group are left handed. Find the probability that 2 or more of a random sample of 25 people are left handed. [Take e-2 = 0.135]
Q. 21. The banker’s gain on a bill due 3 months hence at 5% per annum is Rs. 5.00. Find the sum.
Or
Find the true discount on a bill of Rs. 11,400 due 4 months hence, at 4% per annum.
Q. 22. If the banker’s gain on a bill is 1/9th of the banker’s discount, the rate being 10% per annum, find the unexpired period of the bill.
Q. 23. A, B and C entered into a partnership with the capitals Rs. 5 lac, Rs. 4 lac and Rs. 3 lac respectively, and agreed to share the annual profit in proportion to their capitals. After 5 months A withdrew Rs. 50,000 and B added Rs. 50,000. If at the end of the year the profit was Rs. 1,22,400, calculate their shares in it.
Q. 24. A machine costs a company Rs. 5,25,000 and its effective life is estimated to be 20 years. A sinking fund is created for replacing the machine at the end of its lifetime when its scrap realizes Rs. 25,000 only. Calculate the amount that should be provided every year out of profits, for the sinking fund if it accumulates an interest of 5% per annum compounded annually.
[Use (1.05)20 = 2.65]
Q. 25. The total cost of daily output of x units of an item is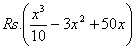 
. Find the output level at which the average cost is minimum. Verify that at this level the average cost and the marginal cost are the same.
Or
A radio manufacturer finds that he can sell x radios per week at the price of Rs. p, where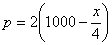 
. If the cost of production of x units per week be 
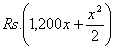. find the number of radios he should produce per week to maximise the profit and also find the profit he will have.
Q. 26. A furniture dealer deals only in two items — tables and chairs. He has Rs. 10,000 to invest and a space to store at most 60 pieces. A table costs him Rs. 500 and a chair Rs. 200. He can sell a table at a profit of Rs. 50 and a chair at a profit of Rs. 15. Assume that he can sell all items that he buys. Using linear programming formulate the problem for maximum profit and solve it graphically.
| Mathematics 2006 Question Papers Class XII | |||||||
| Delhi | Outside Delhi | Compartment Delhi | Compartment Outside Delhi | ||||
 |
Set I | |
Set I | |
Set I | |
Set I |
|
Set II | |
Set II | |
Set II | |
Set II |
|
Set III | |
Set III | ||||
