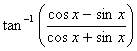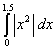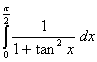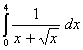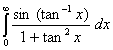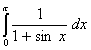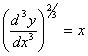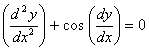CBSE Guess > Papers > Important Questions > Class XII > 2009 > Maths > Mathematics By Mr. Harish Kumar
CBSE CLASS XII
CHAPTER : 1 RELATIONS AND FUNCTIONS
Q. 1.
Q. 2.
Q. 3. If ‘*’ is defined on the set R of all real numbers by 
find the identity element in R w.r.t. *.
Q. 4. If ‘*’ is defined on the set R of all real numbers by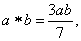 
find the identity element in R for the binary operation *.
Q. 5.
Q. 6. Find the identity element in the set Q+ of positive rational numbers for the operation '' defined by 
Q. 7. Show that the function 
is onto but not one-one.
Q. 8.Show the relation R on the set
is symmetric but neither reflexive nor transitive.
Q. 9.
Q. 10 .
- fog
- gof
Q. 11.
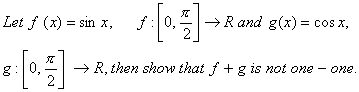
CHAPTER : 2 INVERSE TRIGONOMETRIC FUNCTIONS
Q. 1.
Q. 2.
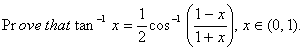
Q. 3.
Q. 4.
Q. 5. 
Q. 6. Find the Value of
Q. 7. Write the following in simplest form :
Q. 8.
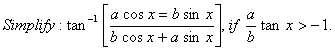
Q. 9. Find the principal value of :
CHAPTER : 3 MATRICES
Q. 1. If a matrix has 8 elements. What are the possible orders it can have? What if it has 5 elements?
Q. 2.
Q. 3.
Q. 4.
Q. 5. Show that the matrix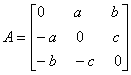 
is skew symmetric.
Q. 6.
Q. 7. Give examples of matrices A and B such that 
Q. 8. Let A be a square matrix. Then check whetherA + AT is a symmetric matrix.
Q. 9. Show that the elements on the main diagonal of a skew symmetric matrix are all zero.
Q. 10. Let A and B be symmetric matrices of same order. Then show that AB - BA is a skew symmetric matrix.
Q. 11. Let A and B be symmetric matrices of same order. Then show that AB + BA is a symmetric matrix.
Q. 12. Give examples of matrices A and B such that 
Q. 13. Show that the matrix BT A B symmetric according as A is symmetric.
Q. 14.
Q. 15.
Q. 16.
CHAPTER : 4 DETERMINANTS
Q. 1.
Q. 2.
Q. 3. Without expanding prove that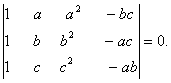 
Q. 4. For what Value of x the matrix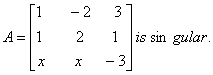 
Q. 5. If A is a matrix of order 3 and |A| = 8 , then find the value of |adj A|
Q. 6. Without expanding evaluate the determinant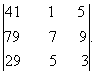 
Q. 7. Find the adjoint of the matrix 
Q. 8. 
Q. 9. 
Find the possible values of x and y, if x, 
Q. 10.
Q. 11.
, then find the value of x.
CHAPTER : 5 CONTINUITY AND DIFFERENTIABILITY
Q. 1.
Q. 2.
Q. 3.
Q. 4.
Q. 5.
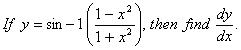
Q. 6. Find the derivative of sin x with respect to log x .
Q. 7.
Q. 8. Find the derivative of x a with respect to x , where a is a positive constant.
Q. 9. If the function f defined by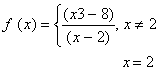 
is continuous at x = 2 , then find the value of k .
Q. 10. Find the value of k , it is given that the function 
CHAPTER : 6 APPLICATION OF DERIVATIVES
Q. 1. Find maximum and minimum values of the function 
Q. 2. Prove that the function 
is neither increasing nor decreasing on (-11).
Q. 3. Find the slope of the tangent to the curve 
Q. 4. The distance moved by a particle traveling in a straight line in t seconds is given by 
. Find the time taken by the particle to come to the rest.
Q. 5. The radius of a circle is increasing at the rate of 0.7 cm/sec. What is the rate of increase of its circumference?
Q. 6. The radius of a circle is increasing at the rate of 0.1 cm/sec. Determine the rate of change of area when radius of the circle is 5cm.
Q. 7. Find the rate of change of volume of a sphere w.r.t. its surface area, when the radius is 2cm.
Q. 8. Show that the function f (x) = 2x + 3 is strictly increasing on R .
Q. 9. Find the equation of the tangent to the curve 
Q. 10. Find the interval on which 
is strictly increasing or decreasing.
Q. 11. For the function 
, find the value of x when y increases 75 times as fast as x .
Q. 12. It is given that at x -1, the function 
attains its maximum value on the interval
. Write the value of a .
CHAPTER : 7 INTEGRALS
Q. 1. Evaluate:
Q. 2. Evaluate:
Q. 3.
Q. 4.
CHAPTER : 8 DIFFERENTIAL EQUATIONS
Q. 1. Find the order of the differential equation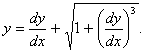 
Q. 2. Find the general solution of the differential equation 
Q. 3. Find the degree and order of the differential equations:
Q. 4. Find the solution of the differential equation 
Q. 5. Find the integrating factor of the differential equation :
CHAPTER : 9 VECTORS
Q. 1.
Q. 2. Find a unit vector perpendicular to both 
Q. 3. For two non zero vectors 
Q. 4.
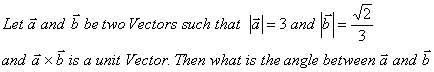
Q. 5. 
Q. 6. Find a unit vector in the direction of 
that has magnitude 7 units.
Q. 7. Find the direction cosines of the vector 
Q. 8. Compute the area of a parallelogram diagonal vectors are 
Q. 9.
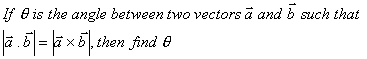
Q. 10.
Q. 11. Find the angle between two vectors having same length 
and their scalar product is -1.
Q. 12.
Q. 13.
Q. 14.
Q. 15.
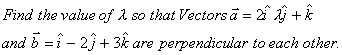
Q. 16.
Q. 17.
Q. 18. Find the projection of the vector 
Q. 19.
CHAPTER : 10 THREE DIMENTIONAL GEOMETRY
Q. 1. Find the direction ratios of the line 6x – 1 = 2y + 3 = 5 – z.
Q. 2. Find the direction cosines of a line making angles 600,900,300with coordinate axes.
Q. 3. Write the direction ratios of the line normal to the plane x+ 2y – 3z + 4 = 0.
Q. 4. Find the direction cosines of y-axis.
Q. 5. Find the equation of a plane making equal intercepts on axes and passing through the point (2,8,3) .
Q. 6. Find the length of the perpendicular from the point (2,3,7) to the plane 3x – y – z = 7.
Q. 7. Write the Cartesian equations of the line passing through (-1,2,3) and equally inclined to the positive direction of x-axis.
Q. 8. Find the angle between the planes 2x -3y + 4z = 1 and –x + y = 4.
Q. 9.
are perpendicular. Find the value of k .
Q. 10. Find the angle between the line 
Q. 11. Find the distance of the point 
Q. 12. Find the angle between the following pair of lines: 
Q. 13. Direction ratios of a line are proportional to (1, -3,2) , then find its direction cosines.
Q. 14. Write the equation of the plane whose intercepts on the coordinate axes are -4,2,3 .
Q. 15. Find the intercepts cut of by the plane 2x + y - z = 5.
CHAPTER : 11 PROBABILITY
Q. 1. An unbiased die is rolled. If the random variable X is defined as 
Find probability distribution of X.
Q. 2. A couple has two children. Find the probability that both children are male, if it is known that one of the children is male.
Q. 3. Events A and B are such that 
State whether
A and B are independent.
Q. 4. In a probability distribution mean is 10 and standard deviation is
. Find the probability of happening of an event.
Q. 5. “Two cards are drawn successively with replacement from a well shuffled pack of 52 cards”. Find the probability distribution of number of queens.In the above statement
- What is the random variable?
- What values a random variable can take?
Q. 6. A random variable X has following probability distribution :
| X | 0 |
1 |
2 |
3 |
P(X) |
0.3 |
k |
0.1 |
2k |
Find k.
Q. 7. A and B are two events such that 
Can you conclude events A and B are independent? Give reason.
Q. 8. In a throw of die the number obtained is an odd number. Find the probability of getting a number less than 6.
Q. 9. In a probability distribution mean is 3 and standard deviation is . Find the probability of non-happening of an event.
Q. 10. For the binomial distribution mean is 4 and variance 6. Is the statement true? Give reason.
Q. 11. A coin is tossed once. Find the probability distribution of number of heads obtained.
Q. 12. A pair of dice is thrown. If the sum is seven. Find the probability that one of the dice shows three.
Q. 13. A die is thrown, if the outcome is an odd number. What is the probability that it is a prime?
Q. 14.
Q. 15.
Q. 16. Probability of a success in an experiment of 4 trials is 
. Find the probability of no success.
Q. 17. The mean and variance of a binomial distribution are 4 and 
respectively. Find 
Q. 18. A die is tossed thrice. Find the probability of getting an odd number at least once.
ANSWERS
CHAPTER : 1 RELATIONS AND FUNCTIONS
-
-
-
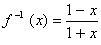
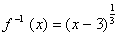
0
-
-
-
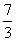
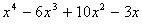
2
-
x
-
(i)
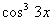
(ii)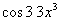
CHAPTER : 2 INVERSE TRIGONOMETRIC FUNCTIONS
5. 
6. i. 
ii. 
7. i. 
ii. 
8. 
9. i. 
ii. 
CHAPTER : 3 MATRICES
1. 
2. 4, 3
3. 
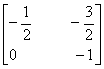
4. 
7. 
14. 
15. x = 3, y = 9, z = -2, w = 20
16. k = 1
CHAPTER : 4 DETERMINANTS
1. 
2. 
4. -1
5. 64
6. 0
7. 
8. x = 4, y = 2; x = 2, y = 4; x = 8, y = 1; x= 1, y = 8
10. m = 3
11. 
CHAPTER : 5 CONTINUITY AND DIFFERENTIABILITY
1. 
2. a = 0
3. 
4. 
5. 
6. 
7. 
8. 
9. k = 12
10 
CHAPTER : 6 APPLICATION OF DERIVATIVES
1. Max value 5, Min value does not exist
3. 
4. 9 sec
5. 1.4 cm/sec.
6. 
7. 1 cm
9. 
10. 
11. 
12. a = 120
CHAPTER : 7 INTEGRALS
1. i. 
ii. 
iii. 
iv. 
v. 
vi. 
2. i. 2
ii. 
iii.
iv. 3
v. 2 log 5
vi. 1
vii. 1
3. 4
4. 37
CHAPTER : 8 DIFFERENTIAL EQUATIONS
1. 1
2. y = xc
3. i. 2, 3
ii. 1, 2
- 2, 3
- 1, 2
- not defined, 2
4. 
5. i. 1 + sinx
ii. 
iii. 
iv. 
CHAPTER : 9 VECTORS
1. 
2. 
3. 
4.
5. 3
6. 
7. 
8. 
9.
10. 
11.
12. - 15
14. 
15. 
16. 20
17. 
18. 
19. 
CHAPTER : 10 THREE DIMENTIONAL GEOMETRY
1. 
2. 
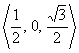
3. 
4. 
5. x + y + z – 13 = 0
6. 
7. x + 1 = y – 2 = z -3
8. 
9. 
10. 
11. 
12. 
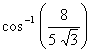
13. 
14. 3x – 6y – 4z + 12 = 0
15. 
CHAPTER : 11 PROBABILITY
1.
| X | 0 |
1 |
P (X) |
|
|
2.
3. Not independent
4. 
5. i. No. of queens
ii. 0, 1, 2
6. k = 0.2
7. 
8. 1
9. 
10. False as Mean > Variance
11.
| X | 0 |
1 |
P (X) |
|
|
12.
13.
14.
15. 0.3
16. 
17. 
18. 
Paper By Harish Kumar PGT Mathematics , JNV Jalandhar, Ph No. 09463647493
