![]()
CBSE Guess > Papers > Important Questions > Class XII > 2009 > Maths > Mathematics By Mr. Munindra Kr. Mazumdar
CBSE CLASS XII
Q. 1. Rate of change of quantities:
- The volume of a spherical balloon is increasing at the rate of 25cm3/sec. Find the rate of change of its surface area at the instant when its radius is 5cm.
- The surface area of a spherical bubble is increasing at the rate of 2cm2/sec. Find the rate at which the volume of the bubble is increasing at the instant its radius is 6cm.
- A balloon which always remains spherical is being inflated by pumping in gas at the rate of 900 cm3/sec . Find the rate at which the radius of the balloon is increasing when the radius of the balloon is 15 cm.
- The volume of a cube is increasing at a rate of 7 cubic centimeters per sec. How fast is the surface area increasing when the length of an edge is 12 cm?
- Water is leaking from a conical funnel at the rate of 5 cm3/sec. If the radius of the base of the funnel is 5 cm and its altitude is 10 cm, find the rate at which the water level is dropping when it is 2.5 cm from the top.
- Two equal sides of an isosceles triangle with fixed base b cm are decreasing at the rate of 3 cm/sec. How fast is the area decreasing when each of the equal sides is equal to the base?
- Find the rate of change of the area of a circle with respect to its radius r when r = 5 cm.
Q. 2. Tangent and Normal :
- If the tangent to the curve
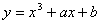 at P(1, -6) is parallel to the line y – x = 5, find the values of a and b.
at P(1, -6) is parallel to the line y – x = 5, find the values of a and b. - Find the equation of the tangent and normal to the curve
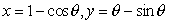 at
at 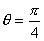
- Find the equation of the tangent and the normal to the curve y = x2 + 4x + 1 at the point whose x - coordinate is 3.
- Find the equation of tangent and normal to the curve x = a cost + at sint, y = a sint – at cost, at any point ‘t”. Also show that the normal to the curve is at a constant distance from origin.
- Prove that the curves x = y2 and xy = k cut each other at right angles if 8k2 = 1
- For the curve y = 4x3 – 2x5 , find all points at which the tangent passes through the origin.
- Find the equation of tangent to the curve
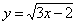 which is parallel to the line
which is parallel to the line 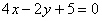
- Find the slope of the curve
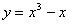 at x = 2
at x = 2
Q.3. Increasing and decreasing function :
- Find the intervals in which the function f(x) =
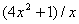 is( a )increasing ( b )decreasing.
is( a )increasing ( b )decreasing. - Find the intervals in which the function f(x) = x3 – 3x2 + 9x + 15 is ( a ) increasing ( b ) decreasing.
- Find the intervals in which the function f given by f(x) = sinx – cosx,
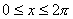 is (i) Increasing (ii) decreasing.
is (i) Increasing (ii) decreasing. - Find the intervals in which the function f(x)=
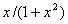 is( a )increasing ( b )decreasing.
is( a )increasing ( b )decreasing. - Find the intervals in which the function f(x) = 2x3 – 15x2 + 36x + 1 is strictly increasing or decreasing. Also find the points on which the tangents are parallel to the x-axis.
- Find the intervals in which the function
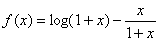 is increasing or decreasing.
is increasing or decreasing. - Find the value of a for which the function
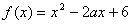 is increasing when x > 0.
is increasing when x > 0. - Find the intervals in which the function
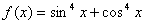 in
in 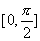 is increasing or decreasing
is increasing or decreasing
Q. 4. Maximum and minimum :
- Show that the maximum volume of the cylinder which can be inscribed in a sphere of radius
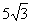 is 500
is 500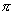 cm3
cm3 - An open box with a square base is to be made out of a given quantity of cardboard of area a2 square units. Find the dimensions of the box so that the volume of the box is maximum. Also find the maximum volume.
- Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is 8/27 of the volume of the sphere.
- A rectangle is inscribed in a semi circle of radius “a’ with one of its sides on the diameter of semi circle. Find the dimensions of the rectangle so that its area is maximum. Find also the area.
- A square piece of tin of side 18 cm is to be made into a box without a top by cutting a square piece from each corner and folding up the flaps. What should be the side of the square to be cut off, So that the volume of the box be maximum. Also find the maximum volume of the box.
- An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of the material will be list when the depth of the tank is half of its width.
- Show that semi vertical angle of the cone of given maximum volume and of given slant height is
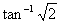
- Show that semi vertical angle of right circular cone of given surface area and maximum volume is
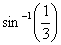 .
. - Show that the height of the cone of maximum volume that can be inscribed in a sphere of radius 12 cm is 16 cm.
- Show that the volume of the greatest right cylinder that can be inscribed in a cone of height h and semi-vertical angle
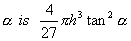
- A beam of length L is supported at one end. If W is the uniform load per unit length, the bending moment M at a distance x from the end is given by
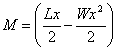 . Find the point on the beam at which the bending moment has the maximum value.
. Find the point on the beam at which the bending moment has the maximum value. - The combined resistance R of two resistors R1 and R2 where R1, R2 > 0is given by
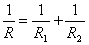 . If R1 + R2 = C (constant) show that the maximum resistance R is obtained by choosing R1 = R2.
. If R1 + R2 = C (constant) show that the maximum resistance R is obtained by choosing R1 = R2.
Q. 6. Approximation :
- Using differentials, find the approximate value of
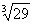
- Using differentials, find the approximate value of
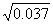
- Using differentials, find the approximate value of
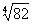
- If y = x4 – 12 and if x changes from 2 to 1.99, when is the approximate change in y?
Paper By Mr. Munindra Kr. Mazumdar
