CBSE Guess > Papers > Important Questions > Class XII > 2008 > Maths > Maths By Mr. Amit Srivastava
CBSE CLASS XII
Section - A
Q. 1. What is the minimum number of factors :
- A prime number can have? (1 marks)
- A composite number can have? (1 marks)
Q. 2. Verify whether x = 3 is a zero of the polynomial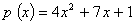 
. Also find the value of p( - 2) (2 marks)
Q. 3. Form a quadratic equation one of whose roots is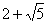 
and the sum of the roots is 4. (2 marks)
Q. 4. Evaluate : 
(2 marks)
Or
If 
then find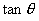 
(2 marks)
Q. 5. Find the value of p for which the equation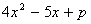 
gives two equal roots. (2 marks)
Q. 6. Given below are three equations. Two of them have infinite solutions and two have unique solutions. State the two pairs. (2 marks)
3x - 2y = 4, 6x + 2y = 4, 9x - 6y = 12
Q. 7. Solve the following equation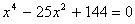 
(2 marks)
Or
Find the sum and product of the roots of the following equation without actually solving it :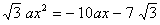 
(2 marks)
Section - B
Q.8. Using Euclid’s Division Lemma, find the HCF of 867 and 255 (3 marks)
Q.9. A fraction becomes 1/3 if 1 is subtracted from both its numerator and denominator. If 1 is added to both numerator and denominator, the fraction becomes 1/2. Find the original fraction. (3 marks)
Or
AThe sum of the digits of a two digit number is 8. If the difference between this number and the number formed by reversing the digits is 18, find the original number. (3 marks)
Q.10. In right triangle ΔPMO, right angled at M, PM = 8cm and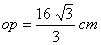 
, find the values of 
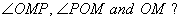(3 marks)
Q.11. Solve for x : 
(3 marks)
Q.12. Find a quadratic polynomial with sum of the roots as 0 and product of the roots as 
(3 marks)
Q.13. Solve for x : 
(3 marks)
Q.14. Solve the following system of equations using elimination method : 
Or
Solve the following system of equations using substitution method : 
Q.15. If 
and 
are the roots are the roots of the quadratic equation x2 + x - 2, find the value of 
without solving for and . (3 marks)
Q.16. For what value of will the following pair of equations have no solution? 
(3 marks)
Q.17. Solve for x and y : 
Hence find a where y = ax - 4. (3 marks)
Q.18. Prove that : 
(3 marks)
Q.19. Show that any positive odd integer is of the form 4m+1 or 4m + 3 where m is any integer. (3 marks)
Section - C
Q.20. Solve the following system of equations graphically and find the coordinates of the points where the lines meet the axis of y. 2(x - 1) = y; x + 3y = 15. (5 marks)
Q.21. A 1.6m tall girl stands at a distance of 3.2 m from a lamp–post and casts a shadow of 4.8m on the ground. Find the height of the lamp–post. (5 marks)
Q.22. Solve for x: 
. (5 marks)
Q.23. Find the quotient and remainder when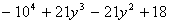 
is divided by 
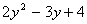. Hence verify the division algorithm. (5 marks)
Q.24. A party of tourists booked a room in a hotel for Rs.1200. Three of the members failed to pay as they had no cash with them. As a result, each of the remaining people had to pay Rs.20 more. How many tourists were there in all?(5 marks)
Or
In a flight of 600km, an aircraft was slowed down due to bad weather. Its average speed for the trip was reduced by 200km/hr and so the time for the journey increased by half an hour. Find the original duration of the flight.
Q.25. Points A and B are 90km apart from each other on a highway. A car starts from A and another from B at the same time. If they go in the same direction, they meet in 9 hours. If they go in opposite directions, they meet in 9/7 hours. Find their speeds. (5 marks)
