CBSE Guess > Papers > Important Questions > Class XI > 2010 > Maths > Maths By Mr. Anil Kumar Tondak

CBSE CLASS XI

Principle of Mathematical Induction

Prove the followings by using Principle of Mathematical Induction:

Q.1. 1 + .

Q.2.

Q.3.

Q.4. 1 + 2 + 3 +-------+ n =

Q.5 . . 12 + 32 + 52 +-----------+(2n – 1)2 =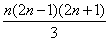

Q.6. 1.3 + 2.4 + 3.5 +--------+n.(n+2) = 1/6 n(n+1)(2n+7)

Q.7. .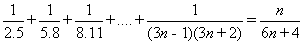

Q.8. 1.2.3 + 2.3.4 + … + n (n + 1) (n+2) = 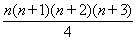for all n ÎN.

Q.9.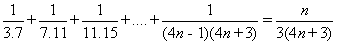

Q.10.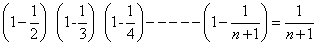

Q.11.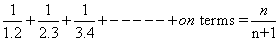

Q.12. 1 + 4 + 7 +-------+(3n-2) =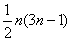

Q.13. 12 + 22 + 32 +---------+ to n term = .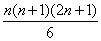

Q.14. 3.6 + 6.9 + 9.12 +--------+3n(3n+3) =3n (n+1) (n+2)

Q.15.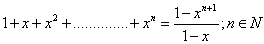

Q.16.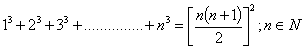

Q.17. 1.3 + 2.32 + 3.32 + … + n.3n = 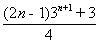for all n ÎN.

Q.18. a + ar + ar2+----------+arn-1=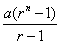

Q.19. Prove : 102n-1 + 1 is divisible by 11.

Q.20. Prove : 2.7n + 3.5n – 5 is divisible by 24 for all n N

Q.21. Prove: 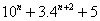is divisible by 9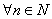

Q.22. Prove: 52n – 1 is divisible by 24 for all n ÎN.

Q.23. Prove: 32n + 7 is divisible by 8 for all n ÎN.

Q.24. Prove: 52n+2 – 24n – 25 is divisible by 576 for all n ÎN.

Q.25. Prove: 72n + 23n – 3 , 3n-1 is divisible by 25 for all n ÎN.

Q.26. Prove: n3 + (n + 1)3 + (n – 2)3 is a multiple of 9

Q.27. Prove: 4n + 15n – 1 is divisible by 9.

Q.28. Prove: 23n – 1 is divisible by 7

Q.29. Prove: 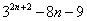is divisible by 64 for every natural number n .

Q.30. Prove: 2.7n + 3.5n – 5 is divisible by 24 for all n ÎN.

Q.31. Prove: 11n + 2 + 122n + 1 is divisible by 133 for all n ÎN.

Q.32. Prove: x2n-1 + y2n-1 is divisible by x + y for all n ÎN.

Q.33. Prove : x2n-1 is divisible by (x – 1)

Q.34. Prove by mathematical induction that 41n – 14n is a multiple of 27.

Q.35. Prove : 1 + 2 + 3 … + n < 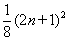for all n ÎN.

Q.36 .Prove: 12 + 22 +----------+n2 > 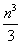, n N.

Q.37. Prove: 3n > n for all nN

Q.38. Prove the rule of exponents (ab)n = an bn

Q.39. Prove by the principle of mathematical induction that: n (n+1) (2n+1) is divisible by 6 for all n Î N

Q.40. If 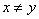then prove that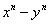is divisible by 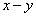for every natural number n.

Q.41 . Prove by induction that (2n + 7) < (n + 3)2 for all natural numbers n. Using this, prove by induction that (n + 3)2 £ 2n+3 for all n ÎN.

Paper By Mr. Anil Kumar Tondak
Email Id : [email protected]
Ph No.: 9811363962